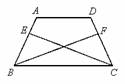
如图 1 ,在 △ ABC 中, ∠ C =90° , ∠ ABC =30° , AC =1 , D 为 △ ABC 内部的一动点(不在边上),连接 BD ,将线段 BD 绕点 D 逆时针旋转 60° ,使点 B 到达点 F 的位置;将线段 AB 绕点 B 顺时针旋转 60° ,使点 A 到达点 E 的位置,连接 AD , CD , AE , AF , BF , EF .
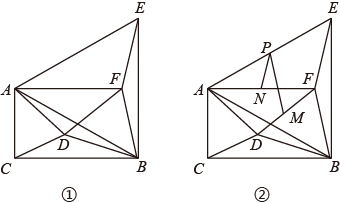
( 1 )求证: △ BDA ≌△ BFE ;
( 2 ) ① CD + DF + FE 的最小值为 ;
② 当 CD + DF + FE 取得最小值时,求证: AD ∥ BF .
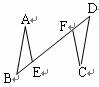
( 3 )如图 2 , M , N , P 分别是 DF , AF , AE 的中点,连接 MP , NP ,在点 D 运动的过程中,请判断 ∠ MPN 的大小是否为定值.若是,求出其度数;若不是,请说明理由.
答案
( 1 )见解答;
( 2 ) ① ; ② 见解答;
( 3 )是, ∠ MPN =30° .
【分析】
( 1 )由旋转 60° 知, ∠ ABD =∠ EBF 、 AB = AE 、 BD = BF ,故由 SAS 证出全等即可;
( 2 ) ① 由两点之间,线段最短知 C 、 D 、 F 、 E 共线时 CD + DF + FE 最小,且 CD + DF + FE 最小值为 CE ,再由 ∠ ACB =90° , ∠ ABC =30° , AC =1 求出 BC 和 AB ,再由旋转知 AB = BE , ∠ CBE =90° ,最后根据勾股定理求出 CE 即可;
② 先由 △ BDF 为等边三角形得 ∠ BFD =60° ,再由 C 、 D 、 F 、 E 共线时 CD + DF + FE 最小, ∠ BFE =120°=∠ BDA ,最后 ADF =∠ ADB -∠ BDF =120°-60°=60° ,即证;
( 3 )由中位线定理知道 MN ∥ AD 且 PN ∥ EF ,再设 ∠ BEF =∠ BAD =α , ∠ PAN =β ,则 ∠ PNF =60° -α+β , ∠ FNM =∠ FAD =60° +α-β ,得 ∠ PNM =120° .
【详解】
解:( 1 )证明: ∵∠ DBF =∠ ABE =60° ,
∴∠ DBF -∠ ABF =∠ ABE -∠ ABF ,
∴∠ ABD =∠ EBF ,
在 △ BDA 与 △ BFE 中,
,
∴△ BDA ≌△ BFE ( SAS );
( 2 ) ①∵ 两点之间,线段最短,
即 C 、 D 、 F 、 E 共线时 CD + DF + FE 最小,
∴ CD + DF + FE 最小值为 CE ,
∵∠ ACB =90° , ∠ ABC =30° , AC =1 ,
∴ BE = AB =2 , BC = ,
∵∠ CBE =∠ ABC +∠ ABE =90° ,
∴ CE = ,
故答案为: ;
② 证明: ∵ BD = BF , ∠ DBF =60° ,
∴△ BDF 为等边三角形,
即 ∠ BFD =60° ,
∵ C 、 D 、 F 、 E 共线时 CD + DF + FE 最小,
∴∠ BFE =120° ,
∵△ BDA ≌△ BFE ,
∴∠ BDA =120° ,
∴∠ ADF =∠ ADB -∠ BDF =120°-60°=60° ,
∴∠ ADF =∠ BFD ,
∴ AD ∥ BF ;
( 3 ) ∠ MPN 的大小是为定值,理由如下:
如图,连接 MN ,
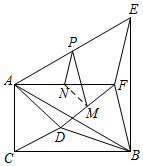
∵ M , N , P 分别是 DF , AF , AE 的中点,
∴ MN ∥ AD 且 PN ∥ EF ,
∵ AB = BE 且 ∠ ABE =60° ,
∴△ ABE 为等边三角形,
设 ∠ BEF =∠ BAD = α , ∠ PAN = β ,
则 ∠ AEF =∠ APN =60°- α , ∠ EAD =60°+ α ,
∴∠ PNF =60°- α + β , ∠ FNM =∠ FAD =60°+ α - β ,
∴∠ PNM =∠ PNF +∠ FNM =60°- α + β +60°+ α - β =120° ,
∵△ BDA ≌△ BFE ,
∴ MN = AD =
FE = PN ,
∴∠ MPN = (180°-∠ PNM )=30° .
【点睛】
本题是三角形与旋转变换的综合应用,熟练掌握旋转的性质、三角形全等的判定与性质、平行线的判定、勾股定理的应用、中位线的性质及等腰、等边三角形的判定与性质是解题关键 .