( 1 )如图 1 ,在 △ABC 中,点 D 、 E 分别是 AB 、 AC 的中点,画出 △ ABC 的中线 AT ;
( 2 )如图 2 ,在 △FGH 中,画出边 GH 的高 FM ,边 GF 的高 HN 和边 FH 的高 GP .
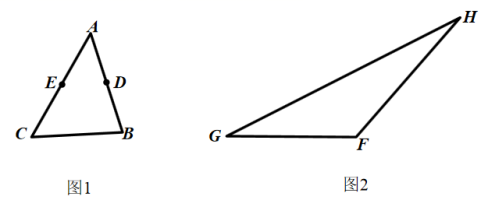
答案
( 1 )见解析;( 2 )见解析
【分析】
( 1 )连接 ,
交于点
,连接
并延长与
交于
,
即为 △ ABC 的中线;
( 2 )用直角三角板的一条直角边与所画的高线的边重合,另一条直角边过另一个顶点,即可作出相应边的高.
【详解】
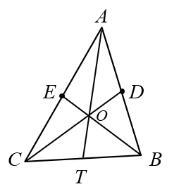
解:( 1 ) △ ABC 的中线 AT 如图所示:
; 
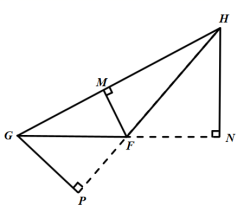
( 2 )边 GH 的高 FM ,边 GF 的高 HN 和边 FH 的高 GP ,如图所示:
. 
【点睛】
本题考查了三角形的中线以及三角形的高,能够根据三角形中线和高的定义画出图形是解题的关键.