如图,在平面直角坐标系 中,抛物线
与 x 轴相交于 O , A 两点,顶点 P 的坐标为
.点 B 为抛物线上一动点,连接
,过点 B 的直线与抛物线交于另一点 C .
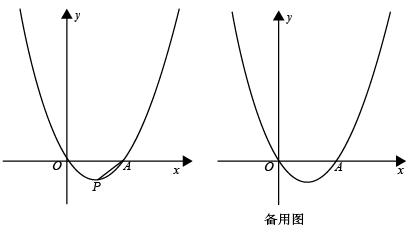
( 1 )求抛物线的函数表达式;
( 2 )若点 B 的横坐标与纵坐标相等, ,且点 C 位于 x 轴上方,求点 C 的坐标;
( 3 )若点 B 的横坐标为 t , ,请用含 t 的代数式表示点 C 的横坐标,并求出当
时,点 C 的横坐标的取值范围.
答案
( 1 ) 或
;( 2 )点 C 的坐标为
或
;( 3 )
;
【分析】
( 1 )设抛物线的解析式为 ,把点 O (0 , 0) 代入即可求解;
( 2 )求得 B (0 , 0) 或 B (8 , 8) ,分两种情况讨论, ① 当点 B 的坐标为 (0 , 0) 时,过点 B 作 BC ∥ AP 交抛物线于点 C ,利用待定系数法求得直线 BC 的解析式为 ,解方程组即可求解; ② 点 B 的坐标为 (8 , 8) 时,作出如图的辅助线,利用三角形函数以及轴对称的性质求得 M (
,
) ,同 ① 可求解;
( 3 )作出如图的辅助线,点 B 的坐标为 ( t , ) ,得到 AH =
, BH =
, OH =
MN ,由 AH =
, BH =
, OH =
MN , △ ABH
△ BMN 得到 M (0 ,
) ,求得 BC 的解析式为:
,解方程组求得点 C 的横坐标为
,即可求解.
【详解】
( 1 ) ∵ 抛物线的顶点坐标为 P (2 , -1) ,
∴ 设抛物线的解析式为 ,
∵ 抛物线经过原点 O ,即经过点 O (0 , 0) ,
∴ ,
解得: ,
∴ 抛物线的解析式为 ;
( 2 )在 中,令
,
得: ,
解得 或
,
∴ B (0 , 0) 或 B (8 , 8) ,
① 当点 B 的坐标为 (0 , 0) 时,过点 B 作 BC ∥ AP 交抛物线于点 C ,
此时 ∠ ABC =∠ OAP ,如图:
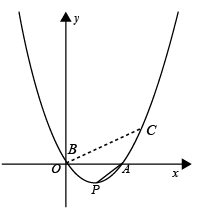
在 中,令
,
得: ,
解得: 或
,
∴ A (4 , 0) ,
设直线 AP 的解析式为 ,
将 A (4 , 0) , P (2 , -1) 代入得
,解得:
,
∴ 直线 AP 的解析式为 ,
∵ BC ∥ AP ,
∴ 设直线 BC 的解析式为 ,
将 B (0 , 0) 代入得 ,
∴ 直线 BC 的解析式为 ,
由 ,
得: ( 此点为点 O ,舍去 ) 或
,
∴ 点 C 的坐标为 (6 , 3) ;
② 点 B 的坐标为 (8 , 8) 时,过点 P 作 PQ ⊥ 轴于点 Q ,过点 B 作 BH ⊥
轴于点 H ,作 H 关于 AB 的对称点 M ,作直线 BM 交抛物线于 C ,连接 AM ,如图:
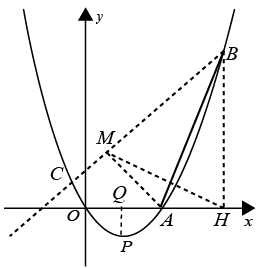
∵ A (4 , 0) , P( 2 , -1) ,
∴ PQ =1 , AQ =2 ,
在 Rt △ APQ 中, ,
∵ A (4 , 0) , B (8 , 8) ,
∴ AH =4 , BH =8 ,
在 Rt △ ABH 中, ,
∴∠ OAP =∠ ABH ,
∵ H 关于 AB 的对称点为 M ,
∴∠ ABM =∠ ABH ,
∴∠ ABC =∠ OAP ,即 C 为满足条件的点,
设 M ( x , y ) ,
∵ H 关于 AB 的对称点为 M ,
∴ AM = AH =4 , BM = BH =8 ,
∴
两式相减得: ,代入即可解得:
( 此点为点 H ,舍去 ) 或
,
∴ M ( ,
) ,
同理求得 BM 的解析式为: ,
解 得:
( 此点为点 B ,舍去 ) 或
,
∴ 点 C 的坐标为 (-1 , ) ;
综上,点 C 的坐标为 (6 , 3) 或 (-1 , ) ;
( 3 )设 BC 交 y 轴于点 M ,过点 B 作 BH ⊥ 轴于点 H ,过点 M 作 MN ⊥
于点 N ,如图:
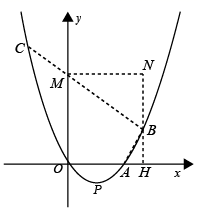
∵ 点 B 的横坐标为 t ,
∴ 点 B 的坐标为 ( t , ) ,又 A (4 , 0) ,
∴ AH = , BH =
, OH =
MN ,
∵∠ ABC =90° ,
∴∠ MBN =90°-∠ ABH =∠ BAH ,
且 ∠ N =∠ AHB =90° ,
∴△ ABH △ BMN ,
∴ ,即
,
∴ BN = ,
∴ HN = ,
∴ M (0 , ) ,
同理求得 BC 的解析式为: ,
由 ,得
,
解得 ( 点 B 的横坐标 ) ,或
,
∴ 点 C 的横坐标为 ,
当 时,
,
∴ 当 时,
的最小值是 12 ,此时
;
∴ 当 时,点 C 的横坐标的取值范围是
.
【点睛】
本题考查二次函数综合知识,涉及解析式、锐角三角函数、对称变换、两条直线平行、两条直线互相垂直、解含参数的方程等,综合性很强,难度较大,解题的关键是熟练掌握、应用各种综合知识,用含字母的式子表示线段长度及函数解析式.

 ,
, ]
] 时,y有最小值且y最小=
时,y有最小值且y最小= ;
;