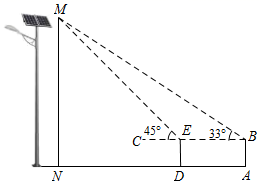
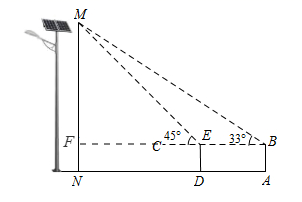
越来越多太阳能路灯的使用，既点亮了城市的风景，也是我市积极落实节能环保的举措．某校学生开展综合实践活动，测量太阳能路灯电池板离地面的高度．如图，已知测倾器的高度为 1.6 米，在测点 A 处安置测倾器，测得点 M 的仰角 ，在与点 A 相距 3.5 米的测点 D 处安置测倾器，测得点 M 的仰角 （点 A ， D 与 N 在一条直线上），求电池板离地面的高度 的长．（结果精确到 1 米；参考数据： ）

答案

8 米

【分析】

过 E 作 EF ⊥ MN 于 F ，连接 EB ，设 MF = x 米，可证四边形 FNDE ，四边形 FNAB 均是矩形，设 MF = EF = x ，可求 FB = x +3.5 ，由 tan∠ MBF = ，解得 米，可求 MN = MF + FN =6.5+1.6≈8 米．

【详解】

解：过 E 作 EF ⊥ MN 于 F ，连接 EB ，设 MF = x 米，

∵∠ EFN =∠ FND =∠ EDN =∠ A =90° ，

∴ 四边形 FNDE ，四边形 FNAB 均是矩形，

∴ FN = ED = AB =1.6 米， AD = BE =3.5 米，

∵∠ MEF =45° ， ∠ EFM =90° ，

∴ MF = EF = x ,

∴ FB = FE + EB = x +3.5 ，

∴tan∠ MBF = ，

∴ 解得 米，

经检验 米符合题意，

∴ MN = MF + FN =6.5+1.6=8.1≈8 米．

【点睛】

本题考查矩形判定与性质，锐角三角函数，简单方程，掌握矩形判定与性质，锐角三角函数，简单方程是解题关键．