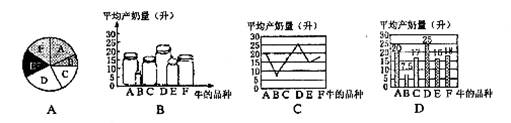
为有效推进儿童青少年近视防控工作,教育部办公厅等十五部门联合制定《儿童青少年近视防控光明行动工作方案( 2021 - 025 年)》,共提出八项主要任务,其中第三项任务为强化户外活动和体育锻炼.我市各校积极落实方案精神,某学校决定开设以下四种球类的户外体育选修课程篮球、足球、排球、乒乓球.为了解学生需求,该校随机对本校部分学生进行了 “ 你选择哪种球类课程 ” 的调查(要求必须选择且只能选择其中一门课程),并根据调查结果绘制成如下不完整的统计图表.
| 课程 | 人数 |
| 篮球 | m |
| 足球 | 21 |
| 排球 | 30 |
| 乒乓球 | n |

根据图表信息,解答下列问题:
( 1 )分别求出表中 m , n 的值;
( 2 )求扇形统计图中 “ 足球 ” 对应的扇形圆心角的度数;
( 3 )该校共有 2000 名学生,请你估计其中选择 “ 乒乓球 ” 课程的学生人数.
答案
( 1 ) m 的值为 36 , n 的值为 33 ;( 2 ) ;( 3 ) 550 人
【分析】
( 1 )由排球人数及其所占百分比可得总人数,再根据总人数乘以篮球的百分比,即可求出篮球的人数,各项目人数之和等于总人数求出乒乓球人数即可;
( 2 )用 360° 乘以对应的比例可得;
( 3 )总人数乘以样本中乒乓球项目人数所占比例.
【详解】
解:( 1 ) ∵ 排球的圆心角 =90°
∴ 排球的百分比为: 25%
参加这次调查的学生人数为 30÷25% = 120 (人),
篮球人数: 120×30%=36
乒乓球人数为 120 ﹣( 36+21+30 )= 33 (人),
所以 m 的值为 36 , n 的值为 33 ;
( 2 )扇形统计图中 “ 足球 ” 项目所对应扇形的圆心角度数为 360° 63° ;
( 3 )估计选择 “ 乒乓球 ” 项目的学生有 2000 550 (人).
【点睛】
本题考查的是条形统计表和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.统计表能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.