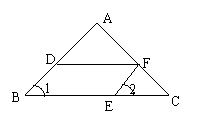
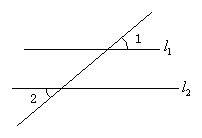
将一副三角板中的两个直角顶点 叠放在一起（如图 ①），其中 ， ， .

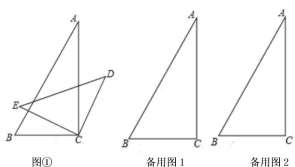
（ 1）猜想 与 的数量关系，并说明理由；

（ 2）若 ，求 的度数；

（ 3）若按住三角板 不动，绕顶点 转动三角 ，试探究 等于多少度时 ，并简要说明理由 .

答案

（ 1） ，理由详见解析；（ 2 ） 135 °；（ 3 ） 等于 或 时， .

【分析】

（ 1 ）依据 ∠ BCD= ∠ ACB+ ∠ ACD=90 ° + ∠ ACD ，即可得到 ∠ BCD+ ∠ ACE 的度数；

（ 2 ）设 ∠ ACE= ，则 ∠ BCD=3 ，依据 ∠ BCD+ ∠ ACE=180 °，即可得到∠ BCD 的度数；

（ 3 ）分两种情况讨论，依据平行线的性质，即可得到当 ∠ BCD 等于 150 °或 30 °时， CE//4B.

【详解】

解：（ 1 ） ，理由如下：

，

；

（ 2 ）如图 ①，设 ，则 ，

由（ 1 ）可得 ，

，

，

；

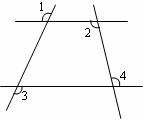
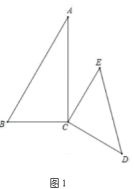
（ 3 ）分两种情况：

①如图 1 所示，当 时， ，

又 ，

；

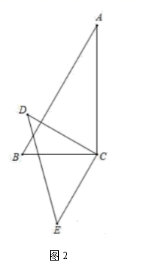
②如图 2 所示，当 时， ，

又 ，

.

综上所述， 等于 或 时， .

【点睛】

本题考查了平行线的判定：同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行 . 熟练掌握定理并且能够准确识图是解题的关键 .