如图,在![]() 和
和![]() 中,
中,![]() ,连接
,连接![]() 交于点
交于点![]() ,连接
,连接![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③
;③![]() 平分
平分![]() ;④
;④![]() 平分
平分![]() .其中正确的个数为( ).
.其中正确的个数为( ).

A.4 B.3 C.2 D.1
答案
B
【分析】
根据题意逐个证明即可,①只要证明![]() ,即可证明
,即可证明![]() ;
;
②利用三角形的外角性质即可证明; ④作![]() 于
于![]() ,
,![]() 于
于![]() ,再证明
,再证明![]() 即可证明
即可证明![]() 平分
平分![]() .
.
【详解】
解:∵![]() ,
,
∴![]() ,
,
即![]() ,
,
在![]() 和
和![]() 中,
中,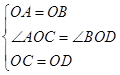 ,
,
∴![]() ,
,
∴![]() ,①正确;
,①正确;
∴![]() ,
,
由三角形的外角性质得:![]()
∴![]() °,②正确;
°,②正确;
作![]() 于
于![]() ,
,![]() 于
于![]() ,如图所示:
,如图所示:
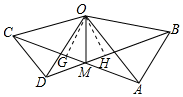
则![]() °,
°,
在![]() 和
和![]() 中,
中,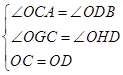 ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 平分
平分![]() ,④正确;
,④正确;
正确的个数有3个;
故选B.
【点睛】
本题是一道几何的综合型题目,难度系数偏上,关键在于利用三角形的全等证明来证明线段相等,角相等.