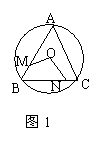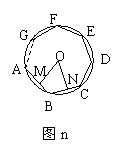半径相等的圆的内接正三角形、正方形、正六边形的边长之比为( )
A.1:![]() :
:![]() B.
B.![]() :
:![]() :1 C.3:2:1 D.1:2:3
:1 C.3:2:1 D.1:2:3
答案
B
【分析】
设圆的半径为R,分别画出圆的内接正三角形、正方形、正六边形,根据锐角三角函数的定义,等腰直角三角形的性质和等边三角形的性质,求出边长即可.
【详解】
设圆的半径为R,
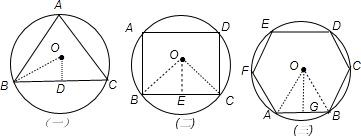
如图(一),
连接OB,过O作OD⊥BC于D,
则∠OBC=30°,BD=OB⋅cos30°=![]() R,
R,
故BC=2BD=![]() R;
R;
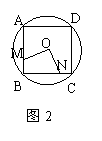
如图(二),
连接OB、OC,过O作OE⊥BC于E,
则△OBE是等腰直角三角形,
2BE2=OB2,即BE=![]() R,
R,
故BC=![]() R;
R;
如图(三),
连接OA、OB,过O作OG⊥AB,
则△OAB是等边三角形,
故AG=OA⋅cos60°=![]() R,AB=2AG=R,
R,AB=2AG=R,
故圆内接正三角形、正方形、正六边形的边长之比为![]() R:
R:![]() R:R=
R:R=![]() :
:![]() :1.
:1.
【点睛】
本题主要考查圆的正多边形的边长,掌握等边三角形的性质和等腰直角三角形的性质是解题的关键.

 。
。