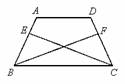
如图，将两个全等的直角三角形△ABD、△ACE拼在一起（图1）．△ABD不动，

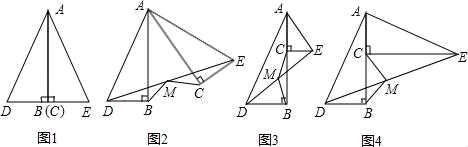
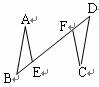
（1）若将△ACE绕点A逆时针旋转，连接DE，M是DE的中点，连接MB、MC（图2），证明：MB＝MC．

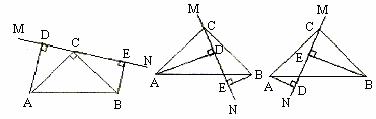
（2）若将图1中的CE向上平移，∠CAE不变，连接DE，M是DE的中点，连接MB、MC（图3），判断并直接写出MB、MC的数量关系．

（3）在（2）中，若∠CAE的大小改变（图4），其他条件不变，则（2）中的MB、MC的数量关系还成立吗？说明理由．

答案

（1）见解析；（2）MB=MC．理由见解析；（3）MB=MC还成立，见解析．

【分析】

（1）连接AM，根据全等三角形的对应边相等可得AD=AE，AB=AC，全等三角形对应角相等可得∠BAD=∠CAE，再根据等腰三角形三线合一的性质得到∠MAD=∠MAE，然后利用“边角边”证明△ABM和△ACM全等，根据全等三角形对应边相等即可得证；
（2）延长DB、AE相交于E′，延长EC交AD于F，根据等腰三角形三线合一的性质得到BD=BE′，然后求出MB∥AE′，再根据两直线平行，内错角相等求出∠MBC=∠CAE，同理求出MC∥AD，根据两直线平行，同位角相等求出∠BCM=∠BAD，然后求出∠MBC=∠BCM，再根据等角对等边即可得证；
（3）延长BM交CE于F，根据两直线平行，内错角相等可得∠MDB=∠MEF，∠MBD=∠MFE，然后利用“角角边”证明△MDB和△MEF全等，根据全等三角形对应边相等可得MB=MF，然后根据直角三角形斜边上的中线等于斜边的一半证明即可．

【详解】

（1）如图（2），连接AM，由已知得△ABD≌△ACE，

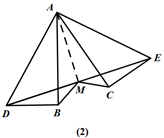
∴AD=AE，AB=AC，∠BAD=∠CAE.

∵MD=ME，

∴∠MAD=∠MAE，

∴∠MAD-∠BAD=∠MAE-∠CAE，

即∠BAM=∠CAM.

在△ABM和△ACM中，

AB=AC，

∠BAM=∠CAM，

AM=AM，

∴△ABM≌△ACM（SAS），

∴MB=MC.

（2）MB=MC．

理由如下：如图（3），延长CM交DB于F，延长BM到G，使得MG=BM，连接CG.

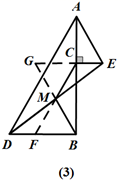
∵CE∥BD，

∴∠MEC=∠MDF，∠MCE=∠MFD.

∵M是ED的中点，

∴MD=ME.

在△MCE和△MFD中，

∠MCE=∠MFD，

∠MEC=∠MDF，

MD=ME，

∴△MCE≌△MFD（AAS）.

∴MF=MC.

∴在△MFB和△MCG中，

MF=MC，

∠FMB=∠CMG，

BM=MG，

∴△MFB≌△MCG（SAS）.

∴FB=GC，∠MFB=∠MCG，

∴CG∥BD，即G、C、E在同一条直线上.

∴∠GCB=90°.

在△FBC和△GCB中，

FB=GC，

∠FBC=∠GCB，

BC=CB，

∴△FBC≌△GCB（SAS）.

∴FC=GB.

∴MB=GB=FC=MC.

（3）MB=MC还成立．

如图（4），延长BM交CE于F，延长CM到G，使得MG=CM，连接BG.

∵CE∥BD，

∴∠MDB=∠MEF，∠MBD=∠MFE.

又∵M是DE的中点，

∴MD=ME.

在△MDB和△MEF中，

∠MDB=∠MEF，

∠MBD=∠MFE，

MD=ME，

∴△MDB≌△MEF（AAS），

∴MB=MF.

∵CE∥BD，

∴∠FCM=∠BGM.

在△FCM和△BGM中，

CM=MG，

∠CMF=∠GMB，

MF=MB，

∴△FCM≌△BGM（SAS）.

∴CF=BG，∠FCM=∠BGM.

∴CF//BG，即D、B、G在同一条直线上.

在△CFB和△BGC中，

CF=BG，

∠FCB=∠GBC，

CB=BC，

∴△CFB≌△BGC（SAS）.

∴BF=CG.

∴MC=CG=BF=MB．

【点睛】

本题考查了全等三角形的判定与性质，等腰三角形三线合一的性质，等角对等边的性质，直角三角形斜边上的中线等于斜边的一半的性质，以及三角形的中位线定理，综合性较强，但难度不大，作辅助线构造出等腰三角形或全等三角形是解题的关键．