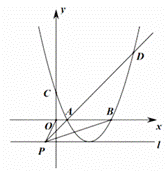
如图所示，二次函数
的图像（记为抛物线
）与y轴交于点C，与x轴分别交于点A、B，点A、B的横坐标分别记为
，
，且
．
（1）若
，
，且过点
，求该二次函数的表达式；
（2）若关于x的一元二次方程
的判别式
．求证：当
时，二次函数
的图像与x轴没有交点．
（3）若
，点P的坐标为
，过点P作直线l垂直于y轴，且抛物线的顶点在直线l上，连接OP、AP、BP，PA的延长线与抛物线交于点D，若
，求
的最小值．
答案
（1）
；（2）见解析；（3）
【解析】
（1）根据题意，把，，点，代入解析式，即可求出解析式；
（2）利用根的判别式进行判断，即可得到结论；
（3）根据二次函数的性质，得到
，结合根与系数的关系，得到
，然后证明
，得到
，然后得到
，利用二次根式的性质即可得到答案．
【详解】
解：（1）由题意得：
，
∵函数过点，
∴
，
∴
，
∴．
（2）由题意，一元二次方程的判别式．
∴
，
∴
，
在函数中，
∵，
∴
，
即函数图象与x轴没有交点．
（3）因为函数顶点在直线l上，则有
，
即①
∵，
∴
，
即
，
∴
，
由①得：②
∵
，
∴
∵
，
∴
，
则．
∴，
∴
，
∴
．
∴
，
∴．
由②得：
，
∴
，
∴当
时，
．
【点睛】
本题考查了二次函数的综合问题，相似三角形的判定和性质，一元二次方程根的判别式，根与系数的关系，解题的关键是熟练掌握相似三角形的判定和性质，二次函数的最值等知识进行解题．
