如图所示，的顶点A在反比例函数的图像上，直线AB交y轴于点C，且点C的纵坐标为5，过点A、B分别作y轴的垂线AE、BF，垂足分别为点E、F，且．

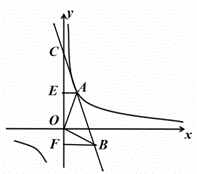
（1）若点E为线段OC的中点，求k的值；

（2）若为等腰直角三角形，，其面积小于3．

①求证：；

②把称为，两点间的“ZJ距离”，记为，求的值．

答案

（1）；（2）①见解析；②8．

【解析】

（1）由点E为线段OC的中点，可得E点坐标为，进而可知A点坐标为：，代入解析式即可求出k；

（2）①由为等腰直角三角形，可得，再根据同角的余角相等可证，由AAS即可证明；

②由“ZJ距离”的定义可知为MN两点的水平距离与垂直距离之和，故，即只需求出B点坐标即可，设点，由可得，进而代入直线AB解析式求出k值即可解答．

【详解】

解：（1）∵点E为线段OC的中点，OC=5，

∴,即：E点坐标为，

又∵AE⊥y轴，AE=1，

∴，

∴．

（2）①在为等腰直角三角形中，，，

∴，

又∵BF⊥y轴，

∴，

∴

在和中

，

∴，

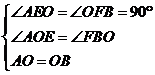②解：设点坐标为，

∵

∴，，

∴，

设直线AB解析式为：，将AB两点代入得：

则．

解得，．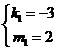

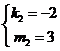当时，，，，符合；

∴

，

当时，，，，不符，舍去；

综上所述：．

【点睛】

此题属于代几综合题，涉及的知识有：反比例函数、一次函数的性质及求法、三角形全等的判定及性质、等腰直角三角形性质等，熟练掌握三角形全等的性质和判定和数形结合的思想是解本题的关键．