AB是
的直径，点C是上一点，连接AC、BC，直线MN过点C，满足
．
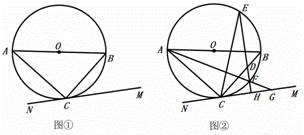
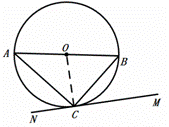
（1）如图①，求证：直线MN是的切线；
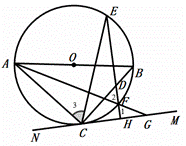
（2）如图②，点D在线段BC上，过点D作
于点H，直线DH交于点E、F，连接AF并延长交直线MN于点G，连接CE，且
，若的半径为1，
，求
的值．
答案
（1）见解析 （2）
【解析】
（1）由圆周角定理的推论和直角三角形的性质可得
，由
可得
，进一步即可推出
，从而可得结论；
（2）如图②，由已知条件易求出AC的长，根据对顶角相等和圆周角定理可得∠1=∠3，根据余角的性质可得
，进而可得
∽
，于是根据相似三角形的性质变形可得
，进一步即可求出结果．
【详解】
解：（1）证明：连接OC，如图，
∵AB是的直径，
∴
，
∴，
∵，
∴，
∵
，
∴，即
，
∴MN是的切线；
（2）如图②，∵
，即
，∴
，
∵∠2=∠3，∠1=∠2，
∴∠1=∠3，
∵，2
∴∠1+∠AGC=90°，
∵∠3+∠ECD=90°，
∴，
又∵
，
∴∽，
∴
，
∴
．
【点睛】
本题考查了圆的切线的判定、等腰三角形的性质、解直角三角形、圆周角定理的推论以及相似三角形的判定和性质等知识，属于常考题型，熟练掌握上述知识、灵活应用相似三角形的判定和性质是解题的关键．
