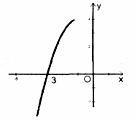
已知函数![]() 均为一次函数,m为常数.
均为一次函数,m为常数.
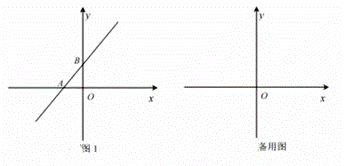
(1)如图1,将直线![]() 绕点
绕点![]() 逆时针旋转45°得到直线
逆时针旋转45°得到直线![]() ,直线
,直线![]() 交y轴于点B.若直线
交y轴于点B.若直线![]() 恰好是
恰好是![]() 中某个函数的图象,请直接写出点B坐标以及m可能的值;
中某个函数的图象,请直接写出点B坐标以及m可能的值;
(2)若存在实数b,使得![]() 成立,求函数
成立,求函数![]() 图象间的距离;
图象间的距离;
(3)当![]() 时,函数
时,函数![]() 图象分别交x轴,y轴于C,E两点,
图象分别交x轴,y轴于C,E两点,![]() 图象交x轴于D点,将函数
图象交x轴于D点,将函数![]() 的图象最低点F向上平移
的图象最低点F向上平移![]() 个单位后刚好落在一次函数
个单位后刚好落在一次函数![]() 图象上,设
图象上,设![]() 的图象,线段
的图象,线段![]() ,线段
,线段![]() 围成的图形面积为S,试利用初中知识,探究S的一个近似取值范围.(要求:说出一种得到S的更精确的近似值的探究办法,写出探究过程,得出探究结果,结果的取值范围两端的数值差不超过0.01.)
围成的图形面积为S,试利用初中知识,探究S的一个近似取值范围.(要求:说出一种得到S的更精确的近似值的探究办法,写出探究过程,得出探究结果,结果的取值范围两端的数值差不超过0.01.)
答案
(1)(0,1);1或0 (2)![]() (3)
(3)![]()
【解析】
(1)由题意,可得点B坐标,进而求得直线![]() 的解析式,再分情况讨论即可解的m值;
的解析式,再分情况讨论即可解的m值;
(2)由非负性解得m和b的值,进而得到两个函数解析式,设![]() 与x轴、y轴交于T,P,
与x轴、y轴交于T,P,![]() 分别与x轴、y轴交于G,H,连接GP,TH,证得四边形GPTH是正方形,求出GP即为距离;
分别与x轴、y轴交于G,H,连接GP,TH,证得四边形GPTH是正方形,求出GP即为距离;
(3)先根据解析式,用m表示出点C、E、D的坐标以及y关于x的表达式为![]() ,得知y是关于x的二次函数且开口向上、最低点为其顶点
,得知y是关于x的二次函数且开口向上、最低点为其顶点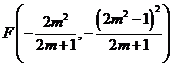 ,根据坐标平移规则,得到关于m的方程,解出m值,即可得知点D 、E的坐标且抛物线过D、E点,观察图象,即可得出S的大体范围,如:
,根据坐标平移规则,得到关于m的方程,解出m值,即可得知点D 、E的坐标且抛物线过D、E点,观察图象,即可得出S的大体范围,如:![]() ,较小的可为平行于DE且与抛物线相切时围成的图形面积.
,较小的可为平行于DE且与抛物线相切时围成的图形面积.
【详解】
解:(1)由题意可得点B坐标为(0,1),
设直线![]() 的表达式为y=kx+1,将点A(-1,0)代入得:k=1,
的表达式为y=kx+1,将点A(-1,0)代入得:k=1,
所以直线![]() 的表达式为:y=x+1,
的表达式为:y=x+1,
若直线![]() 恰好是
恰好是![]() 的图象,则2m-1=1,解得:m=1,
的图象,则2m-1=1,解得:m=1,
若直线![]() 恰好是
恰好是![]() 的图象,则2m+1=1,解得:m=0,
的图象,则2m+1=1,解得:m=0,
综上,![]() ,
,![]() 或者
或者![]()
(2)如图,![]()
![]()
![]() ,
,![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
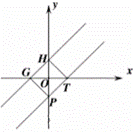
设![]() 与x轴、y轴交于T,P,
与x轴、y轴交于T,P,![]() 分别与x轴、y轴交于G,H,连接GP,TH
分别与x轴、y轴交于G,H,连接GP,TH
![]() ,
,![]()
![]() 四边形GPTH是正方形
四边形GPTH是正方形
![]() ,
,![]() ,即
,即![]()
![]()
![]() ;
;
(3)![]() ,
,![]()
![]() 分别交x轴,y轴于C,E两点
分别交x轴,y轴于C,E两点
![]() ,
,![]()
![]() 图象交x轴于D点
图象交x轴于D点
![]()
![]()
![]()
![]()
![]() 二次函数
二次函数![]() 开口向上,它的图象最低点在顶点
开口向上,它的图象最低点在顶点
![]() 顶点
顶点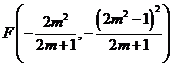
![]() 抛物线顶点F向上平移
抛物线顶点F向上平移![]() ,刚好在一次函数
,刚好在一次函数![]() 图象上
图象上
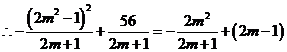 且
且![]()
![]()
![]() ,
,
∴![]() ,
,![]()
![]() 由
由![]() ,
,![]() 得到
得到![]() ,
,![]() ,
,
由![]() 得到与x轴,y轴交点是
得到与x轴,y轴交点是![]() ,
,![]() ,
,![]() ,
,
![]() 抛物线经过
抛物线经过![]() ,
,![]() 两点
两点
![]() 的图象,线段OD,线段OE围成的图形是封闭图形,则S即为该封闭图形的面积
的图象,线段OD,线段OE围成的图形是封闭图形,则S即为该封闭图形的面积
探究办法:利用规则图形面积来估算不规则图形的面积.
探究过程:
①观察大于S的情况.
很容易发现![]()
![]() ,
,![]()
![]()
(若有S小于其他值情况,只要合理,参照赋分.)
②观察小于S的情况.
选取小于S的几个特殊值来估计更精确的S的近似值,取值会因人而不同,下面推荐一种方法,选取以下三种特殊位置:
位置一:如图
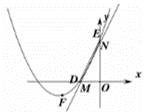
当直线MN与DE平行且与抛物线有唯一交点时,设直线MN与x,y轴分别交于M,N
![]() ,
,![]()
![]() 直线
直线![]()
设直线![]()
![]()
![]()
![]() ,
,![]()
![]() 直线
直线![]()
![]() 点
点![]()
![]()
位置二:如图

当直线DR与抛物线有唯一交点时,直线DR与y轴交于点R
设直线![]() ,
,![]()
![]() 直线
直线![]()
![]()
![]()
![]() ,
,![]()
![]() 直线
直线![]()
![]() 点
点![]()
![]()
位置三:如图
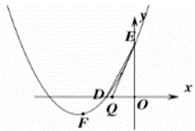
当直线EQ与抛物线有唯一交点时,直线EQ与x轴交于点Q
设直线![]()
![]()
![]()
![]() ,
,![]()
![]() 直线
直线![]()
![]() 点
点![]()
![]()
![]()
我们发现:在曲线DE两端位置时的三角形的面积远离S的值,由此估计在曲线DE靠近中间部分时取值越接近S的值
探究的结论:按上述方法可得一个取值范围![]()
(备注:不同的探究方法会有不同的结论,因而会有不同的答案.只要来龙去脉清晰、合理,即可参照赋分,但若直接写出一个范围或者范围两端数值的差不在0.01之间不得分.)
【点睛】
本题是一道综合性很强的代数与几何相结合的压轴题,知识面广,涉及有旋转的性质、坐标平移规则、非负数的性质、一次函数的图象与性质、二次函数的图象与性质、一元二次方程、不规则图形面积的估计等知识,解答的关键是认真审题,找出相关信息,利用待定系数法、数形结合法等解题方法确定解题思路,利用相关信息进行推理、探究、发现和计算.

 方程有两个不等实数根;
方程有两个不等实数根; 方程有两个相等实数根;
方程有两个相等实数根; 方程没有实数根。
方程没有实数根。 △>0;
△>0; △=0;
△=0; △<0。
△<0。 (△>0)与x轴两交点间的距离的问题。
(△>0)与x轴两交点间的距离的问题。