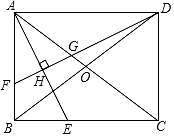
如图，在矩形ABCD中，对角线AC，BD相交于点O，AE平分∠BAC，交BC于点E．作DF⊥AE于点H，分别交AB，AC于点F，G．

（1）判断△AFG的形状并说明理由．

（2）求证：BF＝2OG．

【迁移应用】

（3）记△DGO的面积为S₁，△DBF的面积为S₂，当＝时，求的值．

【拓展延伸】

（4）若DF交射线AB于点F，【性质探究】中的其余条件不变，连结EF，当△BEF的面积为矩形ABCD面积的时，请直接写出tan∠BAE的值．

答案

（1）解：如图1中，△AFG是等腰三角形．

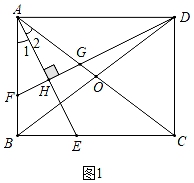
理由：∵AE平分∠BAC，

∴∠1＝∠2，

∵DF⊥AE，

∴∠AHF＝∠AHG＝90°，

∵AH＝AH，

∴△AHF≌△AHG（ASA），

∴AF＝AG，

∴△AFG是等腰三角形．

（2）证明：如图2中，过点O作OL∥AB交DF于L，则∠AFG＝∠OLG．

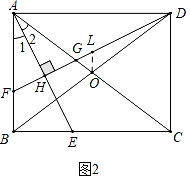
∵AF＝AG，

∴∠AFG＝∠AGF，

∵∠AGF＝∠OGL，

∴∠OGL＝∠OLG，

∴OG＝OL，

∵OL∥AB，

∴△DLO∽△DFB，

∴＝，

∵四边形ABCD是矩形，

∴BD＝2OD，

∴BF＝2OL，

∴BF＝2OG．

（3）解：如图3中，过点D作DK⊥AC于K，则∠DKA＝∠CDA＝90°，

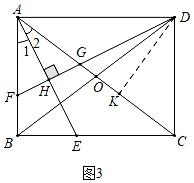
∵∠DAK＝∠CAD，

∴△ADK∽△ACD，

∴＝，

∵S₁＝•OG•DK，S₂＝•BF•AD，

又∵BF＝2OG，＝，

∴＝＝，设CD＝2x，AC＝3x，则AD＝2x，

∴＝＝．

（4）解：设OG＝a，AG＝k．

①如图4中，连接EF，当点F在线段AB上时，点G在OA上．

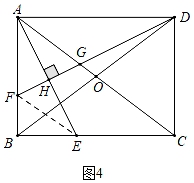
∵AF＝AG，BF＝2OG，

∴AF＝AG＝k，BF＝2a，

∴AB＝k+2a，AC＝2（k+a），

∴AD²＝AC²﹣CD²＝[2（k+a）]²﹣（k+2a）²＝3k²+4ka，

∵∠ABE＝∠DAF＝90°，∠BAE＝∠ADF，

∴△ABE∽△DAF，

∴＝，

∴＝，

∴BE＝，

由题意：10××2a×＝AD•（k+2a），

∴AD²＝10ka，

即10ka＝3k²+4ka，

∴k＝2a，

∴AD＝2a，

∴BE＝＝a，AB＝4a，

∴tan∠BAE＝＝．

②如图5中，当点F在AB的延长线上时，点G在线段OC上，连接EF．

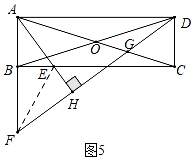
∵AF＝AG，BF＝2OG，

∴AF＝AG＝k，BF＝2a，

∴AB＝k﹣2a，AC＝2（k﹣a），

∴AD²＝AC²﹣CD²＝[2（k﹣a）]²﹣（k﹣2a）²＝3k²﹣4ka，

∵∠ABE＝∠DAF＝90°，∠BAE＝∠ADF，

∴△ABE∽△DAF，

∴＝，

∴＝，

∴BE＝，

由题意：10××2a×＝AD•（k﹣2a），

∴AD²＝10ka，

即10ka＝3k²﹣4ka，

∴k＝a，

∴AD＝a，

∴BE＝＝a，AB＝a，

∴tan∠BAE＝＝，

综上所述，tan∠BAE的值为或．

【分析】（1）如图1中，△AFG是等腰三角形．利用全等三角形的性质证明即可．

（2）如图2中，过点O作OL∥AB交DF于L，则∠AFG＝∠OLG．首先证明OG＝OL，再证明BF＝2OL即可解决问题．

（3）如图3中，过点D作DK⊥AC于K，则∠DKA＝∠CDA＝90°，利用相似三角形的性质解决问题即可．

（4）设OG＝a，AG＝k．分两种情形：①如图4中，连接EF，当点F在线段AB上时，点G在OA上．②如图5中，当点F在AB的延长线上时，点G在线段OC上，连接EF．分别求解即可解决问题．