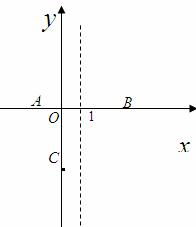
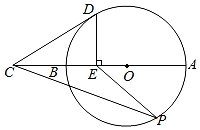
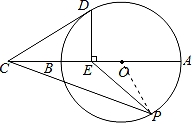
古希腊数学家毕达哥拉斯认为：“一切平面图形中最美的是圆”．请研究如下美丽的圆．如图，线段AB是⊙O的直径，延长AB至点C，使BC＝OB，点E是线段OB的中点，DE⊥AB交⊙O于点D，点P是⊙O上一动点（不与点A，B重合），连接CD，PE，PC．
（1）求证：CD是⊙O的切线；
（2）小明在研究的过程中发现
是一个确定的值．回答这个确定的值是多少？并对小明发现的结论加以证明．
答案
解：（1）连接OD、DB，
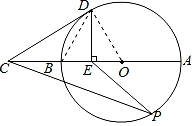
∵点E是线段OB的中点，DE⊥AB交⊙O于点D，
∴DE垂直平分OB，
∴DB＝DO．
∵在⊙O中，DO＝OB，
∴DB＝DO＝OB，
∴△ODB是等边三角形，
∴∠BDO＝∠DBO＝60°，
∵BC＝OB＝BD，且∠DBE为△BDC的外角，
∴∠BCD＝∠BDC＝
∠DBO．
∵∠DBO＝60°，
∴∠CDB＝30°．
∴∠ODC＝∠BDO+∠BDC＝60°+30°＝90°，
∴CD是⊙O的切线；
（2）答：这个确定的值是．
连接OP，如图：
由已知可得：OP＝OB＝BC＝2OE．
∴
＝
＝，
又∵∠COP＝∠POE，
∴△OEP∽△OPC，
∴＝＝．
【分析】（1）连接OD、DB，由已知可知DE垂直平分OB，则DB＝DO，再由圆的半径相等，可得DB＝DO＝OB，即△ODB是等边三角形，则∠BDO＝60°，再由等腰三角形的性质及三角形的外角性质可得∠CDB＝30°，从而可得∠ODC＝90°，按照切线的判定定理可得结论；
（2）连接OP，先由已知条件得OP＝OB＝BC＝2OE，再利用两组边成比例，夹角相等来证明△OEP∽△OPC，按照相似三角形的性质得出比例式，则可得答案．
