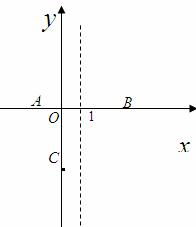
如图，二次函数y=ax²+bx+c（a＞0）的图象与x轴交于两点（x₁，0），（2，0），其中0＜x₁＜1．下列四个结论：①abc＜0；②2a-c＞0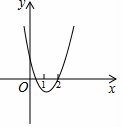；③a+2b+4c＞0；④+＜-4，正确的个数是（　　）

A. 1
B. 2
C. 3
D. 4

答案

D
【解析】

解：①∵抛物线开口向上，
∴a＞0，
∵抛物线对称轴在y轴的右侧，
∴b＜0，
∵抛物线与y轴的交点在x轴上方，
∴c＞0，
∴abc＜0，所以①正确；
②∵图象与x轴交于两点（x₁，0），（2，0），其中0＜x₁＜1，
∴＜-＜，
∴1＜-＜，
当-＜时，b＞-3a，
∵当x=2时，y=4a+2b+c=0，
∴b=-2a-c，
∴-2a-c＞-3a，
∴2a-c＞0，故②正确；
③∵-，
∴2a+b＞0，
∵c＞0，
4c＞0，
∴a+2b+4c＞0，
故③正确；
④∵-，
∴2a+b＞0，
∴（2a+b）²＞0，
4a²+b²+4ab＞0，
4a²+b²＞-4ab，
∵a＞0，b＜0，
∴ab＜0，dengx
∴，
即，
故④正确．
故选：D．
二次函数y=ax²+bx+c（a≠0）①二次项系数a决定抛物线的开口方向和大小．
当a＞0时，抛物线向上开口；当a＜0时，抛物线向下开口；|a|还可以决定开口大小，|a|越大开口就越小．
②一次项系数b和二次项系数a共同决定对称轴的位置．当a与b同号时（即ab＞0），对称轴在y轴左；当a与b异号时（即ab＜0），对称轴在y轴右．（简称：左同右异）
③常数项c决定抛物线与y轴交点．抛物线与y轴交于（0，c）．
本题考查了二次函数图象与系数关系，熟练掌握二次函数图象的性质是解题的关键．