如图,抛物线y=ax2+6ax(a为常数,a>0)与x轴交于O,A两点,点B为抛物线的顶点,点D的坐标为(t,0)(﹣3<t<0),连接BD并延长与过O,A,B三点的⊙P相交于点C.
(1)求点A的坐标;
(2)过点C作⊙P的切线CE交x轴于点E.
①如图1,求证:CE=DE;
②如图2,连接AC,BE,BO,当a=,∠CAE=∠OBE时,求﹣的值.
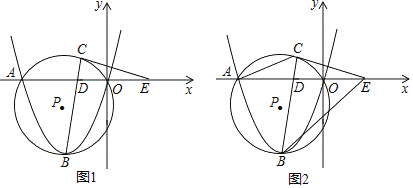
答案
【解答】解:(1)令ax2+6ax=0,
ax(x+6)=0,
∴A(﹣6,0);
(2)①证明:如图,连接PC,连接PB延长交x轴于点M,
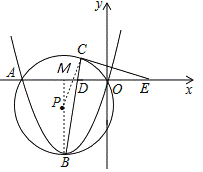
∵⊙P过O、A、B三点,B为顶点,
∴PM⊥OA,∠PBC+∠BOM=90°,
又∵PC=PB,
∴∠PCB=∠PBC,
∵CE为切线,
∴∠PCB+∠ECD=90°,
又∵∠BDP=∠CDE,
∴∠ECD=∠COE,
∴CE=DE.
②解:设OE=m,即E(m,0),
由切割线定理得:CE2=OE•AE,
∴(m﹣t)2=m•(m+6),
∴![]() ①,
①,
∵∠CAE=∠CBD,
∠CAE=∠OBE,∠CBO=∠EBO,
由角平分线定理:,
即:![]() ,
,
∴②,
由①②得![]() ,
,
整理得:t2+18t+36=0,
∴t2=﹣18t﹣36,
∴![]() .
.