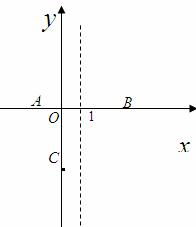
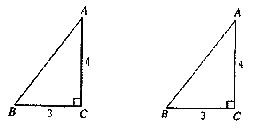
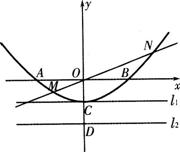
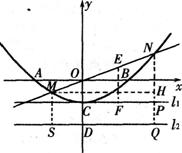
如图，已知抛物线与坐标轴分别交于A(-2，O)、B(2，0)、C(0，-l)三点，过坐标原点0的直线y=kx与抛物线交
于M、N两点．分别过点C,D(0，-2)作平行于x轴的直线
．
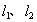(1)求抛物线对应二次函数的解析式；
(2)求证以ON为直径的圆与直线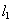
相切；
(3)求线段MN的长(用k表示)，并证明M、N两点到直线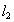
的距离之和等于线段MN的长．
答案
解：(1)设抛物线对应二次函数的解析式为y=ax2+bx+c，
由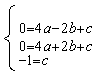
解得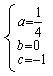
所以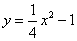
．………………………………………………………3分
(2)设M(x1，y1)，N(x2，y2)，因为点M、N在抛物线上，
所以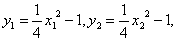
，所以x22=4(y2+1)；
又ON2=x22+y22=4(y2+1)+y22=(y2+2)2，所以ON=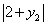
，又因为y2≥-l，
所以0N=2+y2．………………………………………5分
设ON的中点E，分别过点N、E向直线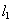作垂线，垂足为P、F，
则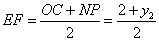 
，
所以ON=2EF，
即ON的中点到直线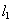，的距离等于0N长度的一半，
所以以ON为直径的圆与相切．………………………………………7分
(3)过点M作MH⊥NP交NP于点H，则MN2=MH2+NH2=(x2-x1)2+(y2-y1)，
又y1=kx1,y2=kx2，所以（y2-y1)2=k2(x2-x1)2
所以MN2=(1+k2)(x2一xl)2；
又因为点M、N既在y=kx的图象上又在抛物线上，
所以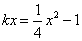
，即x2-4kx-4=0，
所以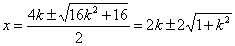
，
所以(x2-x1)2=16(1+k2)，
所以MN2=16(1+k2)2，∴MN=4(1+k2)…9分
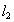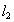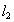延长NP交于点Q，过点M作MS⊥交于点S，
则MS+NQ=y1+2+y2+2=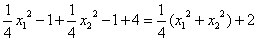
又x12+x22=2[4k2+4(1+k2)]=16k2+8，
所以MS+NQ=4k2+2+2=4(1+k2)=MN
即M、N两点到距离之和等于线段MN的长．……………………ll分
