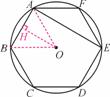
如图,正六边形ABCDEF为⊙O的内接正六边形,连接AE.已知⊙O的半径为2cm.()求∠A∈D的度数和cosuPC(OAB的长;(2)求正六边形ABCDEF⊙O的面积之比

当前位置：

学科首页

九上第二十四章圆

正多边形和圆

试题详情

难度：

使用次数：169

更新时间：2021-04-28

纠错

如图，正六边形ABCDEF为⊙O的内接正六边形，连接AE.已知⊙O的半径为2 cm.

(1)求∠AED的度数和的长；

(2)求正六边形ABCDEF与⊙O的面积之比．

查看答案

题型：解答题

知识点：正多边形和圆

下载试题

复制试题

【答案】

解：(1)连接OA，OB.

∵ABCDEF为正六边形，

∴∠F＝120°，∠AEF＝30°.

∴∠AED＝120°－30°＝90°.

∴∠AOB＝360°×＝60°，

的长为＝ cm.

(2)过点O作OH⊥AB，垂足为H，

∵∠AOH＝30°，OA＝2 cm，

∴由勾股定理得OH＝ cm，S_△AOB＝AB·OH＝×2×＝(cm²)．

∴正六边形ABCDEF的面积为6S_△AOB＝6 cm²，⊙O的面积为π·2²＝4π cm².

∴正六边形ABCDEF与⊙O的面积之比＝6∶4π＝3∶2π.

考点梳理:

根据可圈可点权威老师分析，试题“ ”主要考查你对正多边形和圆（内角，外角，中心角，边心距，边长，周长，面积的计算）等考点的理解。关于这些考点的“资料梳理”如下：

◎ 正多边形和圆（内角，外角，中心角，边心距，边长，周长，面积的计算）的定义

正多边形的定义：
各边相等，各角也相等的多边形叫做正多边形。

正多边形和圆的关系：
把一个圆分成n等份，依次连接各分点所得的多边形是这个圆的内接正n边形，这个圆叫这个正n边形的外接圆。

与正多边形有关的概念：
（1）正多边形的中心：正多边形的外接圆的圆心叫做这个正多边形的中心。
（2）正多边形的半径：正多边形的外接圆的半径叫做这个正多边形的半径。
（3）正多边形的边心距：正多边形的中心到正多边形一边的距离叫做这个正多边形的边心距。
（4）正多边形的中心角：正多边形的每一边所对的外接圆的圆心角叫做这个正多边形的中心角。
注：正n边形有n个中心角，这n个中心角相等且每个中心角为

。

◎ 正多边形和圆（内角，外角，中心角，边心距，边长，周长，面积的计算）的知识扩展

1、正多边形的定义：各边相等，各角也相等的多边形叫做正多边形。
2、正多边形和圆的关系：把一个圆分成n等份，依次连接各分点所得的多边形是这个圆的内接正n边形，这个圆叫这个正n边形的外接圆。
3、与正多边形有关的概念：
（1）正多边形的中心：正多边形的外接圆的圆心叫做这个正多边形的中心。
（2）正多边形的半径：正多边形的外接圆的半径叫做这个正多边形的半径。
（3）正多边形的边心距：正多边形的中心到正多边形一边的距离叫做这个正多边形的边心距。
（4）正多边形的中心角：正多边形的每一边所对的外接圆的圆心角叫做这个正多边形的中心角。
注：正n边形有n个中心角，这n个中心角相等且每个中心角为

。

◎ 正多边形和圆（内角，外角，中心角，边心距，边长，周长，面积的计算）的特性

圆的计算公式：
1.圆的边长即的周长C=2πr=或C=πd
2.圆的面积S=πr2
3.扇形弧长L=圆心角（弧度制）· r = n°πr/180°（n为圆心角）
4.扇形面积S=nπ r²/360=Lr/2（L为扇形的弧长）
5.圆的直径 d=2r
6.圆锥侧面积 S=πrl（l为母线长）
7.圆锥底面半径 r=n°/360°L（L为母线长）（r为底面半径）
8.圆心角所对的弧的度数等于弧所对的圆心角的度数;
9.圆周角的度数等于圆心角的度数的一半;
10.圆外角的度数等于圆外角所对的长弧的度数与短弧的度数的差的一半；
11.扇形圆心角n=（180L）/（πr）（度）。

◎ 正多边形和圆（内角，外角，中心角，边心距，边长，周长，面积的计算）的教学目标

1、了解正多边形的概念、正多边形和圆的关系。
2、会通过等分圆心角的方法等分圆周，画出所需的正多边形。
3、能够用直尺和圆规作图，作出一些特殊的正多边形。
4、理解正多边形的中心、半径、边心距、中心角等概念。

◎ 正多边形和圆（内角，外角，中心角，边心距，边长，周长，面积的计算）的考试要求

能力要求：理解
课时要求：70
考试频率：常考
分值比重：3

开通会员

登录并加入会员可无限制查看知识点解析

类题推荐：

正多边形和圆

难度：

使用次数：71

更新时间：2009-03-15

加入组卷