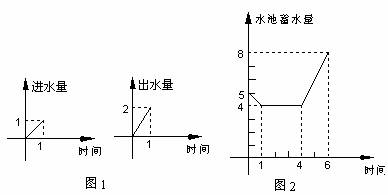
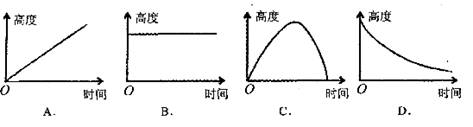
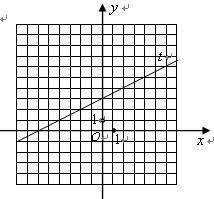
如图,一次函数![]() 的图象与
的图象与![]() 轴、
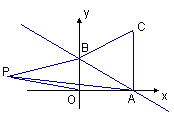
轴、![]() 轴分别交于点A、B,以线段AB为边在第一象限内作等边△ABC,
轴分别交于点A、B,以线段AB为边在第一象限内作等边△ABC,
(1) 求△ABC的面积;
(2) 如果在第二象限内有一点P(![]() ),试用含
),试用含![]() 的式子表示四边形ABPO的面积,并求出当△ABP的面积与△ABC的面积相等时
的式子表示四边形ABPO的面积,并求出当△ABP的面积与△ABC的面积相等时![]() 的值;
的值;
(3) 在![]() 轴上,存在这样的点M,使△MAB为等腰三角形.请直接写出所有符合要求的点M的坐标.
轴上,存在这样的点M,使△MAB为等腰三角形.请直接写出所有符合要求的点M的坐标.
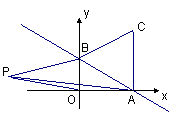
答案
解:根据条件,A、B两点的坐标分别是(![]() )、(
)、(![]() ).
).
(1) 在△ABO中,由勾股定理,得![]() .
.
所以正△ABC的高是![]() ,从而△ABC的面积是
,从而△ABC的面积是![]() .
.
(2) 过P作PD垂直OB于D,则四边形ABPO的面积
![]() .
.
当△ABP的面积与△ABC的面积相等时,
四边形ABPO的面积-△AOP的面积=△ABC的面积,
![]() 即
即![]() .
.
解得![]() .
.
(3) 符合要求的点M的坐标分别是(![]() )、(
)、(![]() )、(
)、(![]() )、(
)、(![]() ).
).