阅读理解：在平面直角坐标系中，若两点P、Q的坐标分别是P（x₁，y₁）、

Q（x₂，y₂），则P、Q这两点间的距离为|PQ|=．如P（1，2），Q（3，4），则|PQ|==2．

对于某种几何图形给出如下定义：符合一定条件的动点形成的图形，叫做符合这个条件的点的轨迹．如平面内到线段两个端点距离相等的点的轨迹是这条线段的垂直平分线．

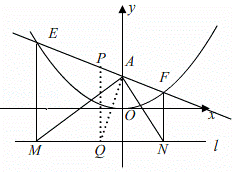
解决问题：如图，已知在平面直角坐标系xOy中，直线y=kx+交y轴于点A，点A关于x轴的对称点为点B，过点B作直线l平行于x轴．

（1）到点A的距离等于线段AB长度的点的轨迹是　x²+（y﹣）²=1　；

（2）若动点C（x，y）满足到直线l的距离等于线段CA的长度，求动点C轨迹的函数表达式；

问题拓展：（3）若（2）中的动点C的轨迹与直线y=kx+交于E、F两点，分别过E、F作直线l的垂线，垂足分别是M、N，求证：①EF是△AMN外接圆的切线；②+为定值．

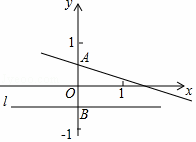
答案

【解答】解：（1）设到点A的距离等于线段AB长度的点D坐标为（x，y），

∴AD²=x²+（y﹣）²，

∵直线y=kx+交y轴于点A，

∴A（0，），

∵点A关于x轴的对称点为点B，

∴B（0，﹣），

∴AB=1，

∵点D到点A的距离等于线段AB长度，

∴x²+（y﹣）²=1，

故答案为：x²+（y﹣）²=1；

（2）∵过点B作直线l平行于x轴，

∴直线l的解析式为y=﹣，

∵C（x，y），A（0，），

∴AC²=x²+（y﹣）²，点C到直线l的距离为：（y+），

∵动点C（x，y）满足到直线l的距离等于线段CA的长度，

∴x²+（y﹣）²=（y+）²，

∴动点C轨迹的函数表达式y=x²，

（3）①如图，

设点E（m，a）点F（n，b），

∵动点C的轨迹与直线y=kx+交于E、F两点，

∴，

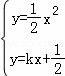∴x²﹣2kx﹣1=0，

∴m+n=2k，mn=﹣1，

∵过E、F作直线l的垂线，垂足分别是M、N，

∴M（m，﹣），N（n，﹣），

∵A（0，），

∴AM²+AN²=m²+1+n²+1=m²+n²+2=（m+n）²﹣2mn+2=4k²+4，

MN²=（m﹣n）²=（m+n）²﹣4mn=4k²+4，

∴AM²+AN²=MN²，

∴△AMN是直角三角形，MN为斜边，

取MN的中点Q，

∴点Q是△AMN的外接圆的圆心，

∴Q（k，﹣），

∵A（0，），

∴直线AQ的解析式为y=﹣x+，

∵直线EF的解析式为y=kx+，

∴AQ⊥EF，

∴EF是△AMN外接圆的切线；

②证明：∵点E（m，a）点F（n，b）在直线y=kx+上，

∴a=mk+，b=nk+，

∵ME，NF，EF是△AMN的外接圆的切线，

∴AE=ME=a+=mk+1，AF=NF=b+=nk+1，

∴+=+====2，

即：+为定值，定值为2．

【点评】此题是圆的综合题，主要考查了待定系数法，两点间的距离公式，直角三角形的判定和性质，根与系数的关系，圆的切线的判定和性质，利用根与系数的确定出m+n=2k，mn=﹣1是解本题是关键．