.如图，在四边形ABCD中，∠B=60°，∠D=30°，AB=BC．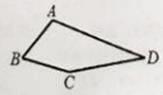

（1）求∠A+∠C的度数。   

（2）连接BD，探究AD，BD，CD三者之间的数量关系，并说明理由。   

（3）若AB=1，点E在四边形ABCD内部运动，且满足 ，求点E运动路径的长度。   

答案

（1）解：在四边形ABCD中，∠B=60°，∠D=30°，
∴∠A+∠C=360°-∠B-∠C=360°-60°-30°=270°。
（2）解：如图，将△BCD绕点B逆时针旋转60°，得到△BAQ，连接DQ，

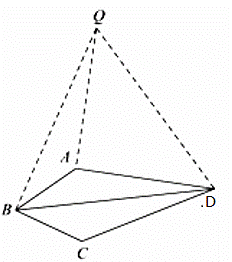
∵BD=BQ，∠DBQ=60°，
∴△BDQ是等边三角形，
∴BD=DQ，
∵∠BAD+∠C=270°，
∴∠BAD+∠BAQ=270°，
∴∠DAQ=360°-270°=90°，
∴△DAQ是直角三角形
∴AD²+AQ²=DQ²  ，
即AD²+CD²=BD²
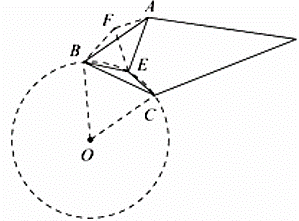
（3）解：如图，将△BCE绕点B逆时针旋转60°，得到△BAF，连接EF，

∵BE=BF，∠EBF=60°，
∴△BEF是等边三角形，
∴EF=BE，∠BFE=60°，
∵AE²=BE²+CE²
∴AE²=EF²+AF²
∴∠AFE=90°
∴∠BFA=∠BFE+∠AFE=60°+90°=150°，
∴∠BEC=150°，
则动点E在四边形ABCD内部运动，满足∠BEC=150°，以BC为边向外作等边△OBC，
则点E是以O为圆心，OB为半径的圆周上运动，运动轨迹为BC，
∵OB=AB=1，
则BC= =

【考点】等边三角形的判定与性质，勾股定理的逆定理，多边形内角与外角，弧长的计算，旋转的性质  

【解析】【分析】（1）根据四边形内角和为360度，结合已知条件即可求出答案.
（2）将△BCD绕点B逆时针旋转60°，得到△BAQ，连接DQ（如图），由旋转性质和等边三角形判定得△BDQ是等边三角形，由旋转性质根据角的计算可得△DAQ是直角三角形，根据勾股定理得AD²+AQ²=DQ²  ， 即AD²+CD²=BD².
（3）将△BCE绕点B逆时针旋转60°，得到△BAF，连接EF(如图)，由等边三角形判定得△BEF是等边三角形，结合已知条件和等边三角形性质可得AE²=EF²+AF²  ， 即∠AFE=90°，从而得出∠BFA=∠BEC=150°，从而得出点E是在以O为圆心，OB为半径的圆周上运动，运动轨迹为BC，根据弧长公式即可得出答案.