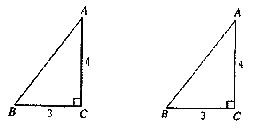
甲、乙两个机器人检测零件，甲比乙每小时多检测20个，甲检测300个比乙检测200个所用的时间少10％，若设甲每小时检x个，则根据题意，可列处方程：________。   

16.如图，在矩形ABCD中，AB=4，AD=2，点E在CD上，DE=1，点F是边AB上一动点，以EF为斜边作Rt△EFP．若点P在矩形ABCD的边上，且这样的直角三角形恰好有两个，则AF的值是________。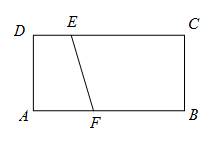

答案

0或1＜AF＜ 或4 

【考点】矩形的性质，圆周角定理，切线的性质，直角三角形的性质  

【解析】【解答】解：以EF为斜边的直角三角形的直角顶点P是以EF为直径的圆与矩形边的交点，取EF的中点O，
（1）如图1，当圆O与AD相切于点G时，连结OG，此时点G与点P重合，只有一个点，此时AF=OG=DE=1；

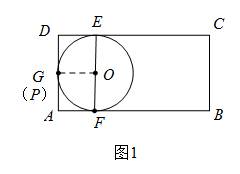
（2）如图2，当圆O与BC相切于点G，连结OG，EG，FG，此时有三个点P可以构成Rt△EFP，
 
∵OG是圆O的切线，
∴OG⊥BC
∴OG//AB//CD
∵OE=OF，
∴BG=CG，
∴OG=（BF+CE），
设AF=x，则BF=4-x，OG=(4-x+4-1)=(7-x)，
则EF=2OG=7-x，EG²=EC²+CG²=9+1=10,FG²=BG²+BF²=1+(4-x)²
在Rt△EFG中，由勾股定理得EF²=EG²+FG²  ， 得（7-x）²=10+1+（4-x）²,解得x=
所以当1＜AF＜时，以EF为直径的圆与矩形ABCD的交点（除了点E和F）只有两个；
（3）因为点F是边AB上一动点：
当点F与A点重合时，AF=0，此时Rt△EFP正好有两个符合题意；
当点F与B点重合时，AF=4，此时Rt△EFP正好有两个符合题意；
故答案为0或1＜AF＜或4
【分析】学习了圆周角的推论：直径所对的圆周角是直角，可提供解题思路，不妨以EF为直径作圆，以边界值去讨论该圆与矩形ABCD交点的个数