平面直角坐标系xOy中，二次函数y=x2﹣2mx+m2+2m+2的图象与x轴有两个交点．
（1）当m=﹣2时，求二次函数的图象与x轴交点的坐标；
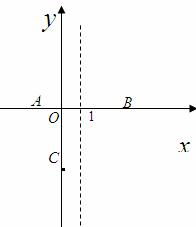
（2）过点P（0，m﹣1）作直线1⊥y轴，二次函数图象的顶点A在直线l与x轴之间（不包含点A在直线l上），求m的范围；
（3）在（2）的条件下，设二次函数图象的对称轴与直线l相交于点B，求△ABO的面积最大时m的值．
答案
【分析】（1）与x轴相交令y=0，解一元二次方程求解；
（2）应用配方法得到顶点A坐标，讨论点A与直线l以及x轴之间位置关系，确定m取值范围．
（3）在（2）的基础上表示△ABO的面积，根据二次函数性质求m．
【解答】解：（1）当m=﹣2时，抛物线解析式为：y=x2+4x+2
令y=0，则x2+4x+2=0
解得x1=﹣2+
，x2=﹣2﹣
抛物线与x轴交点坐标为：（﹣2+，0）（﹣2﹣，0）
（2）∵y=x2﹣2mx+m2+2m+2=（x﹣m）2+2m+2
∴抛物线顶点坐标为A（m，2m+2）
∵二次函数图象的顶点A在直线l与x轴之间（不包含点A在直线l上）
∴当直线1在x轴上方时
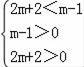
不等式无解
当直线1在x轴下方时
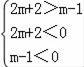
解得﹣3＜m＜﹣1
（3）由（1）
点A在点B上方，则AB=（2m+2）﹣（m﹣1）=m+3
△ABO的面积S=
（m+3）（﹣m）=﹣
∵﹣
∴当m=﹣
时，S最大=
【点评】本题以含有字母系数m的二次函数为背景，考查了二次函数图象性质以及分类讨论、数形结合的数学思想．
