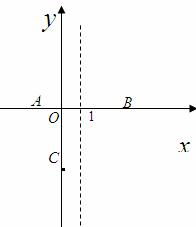
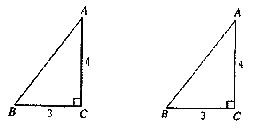
小敏思考解决如下问题：
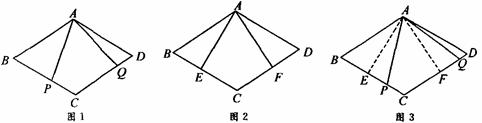
原题：如图1，点
，
分别在菱形
的边
，
上，
，求证：
.
[来源~:中&*^@教网]
(1) 小敏进行探索，若将点，的位置特殊化，把
绕点
旋转得到
，使
，点
分别在边
上，如图2，此时她证明了
.请你证明.
(2) 受以上(1)的启发，在原题中，添加辅助线：如图3，作
，
，垂足分别为，请你继续完成原题的证明.
(3) 如果在原题中添加条件：
，
，如图1，请你编制一个计算题(不标注新的字母)，并直线给出答案.
答案
解：(1)当
为顶角，则
，
当为底角，若
为顶角，则
，
若为底角，则
.
∴或
或
.
(2)分两种情况：
①当
时，只能为顶角，
∴的度数只有一个.
②当
时，
若为顶角，则
，
若为底角，则
或
，
当
且
，且
，即
时，
有三个不同的度数.
综上①②，当且时，有三个不同的度数.
23.解：(1)如图1，
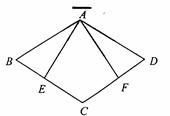
在菱形中，
，
，
，
∵
，
∴
，
∴
，
∵，
∴
，
∴
，
，
∴
.
∴.
(2)如图2，由(1)，∵
，
∴
，
∵，，
∴
，
∵，
∴
，
∴.
(3)不唯一，举例如下：
层次1：①求
的度数，答案：
.
②分别求
，
的度数.答案：
.
③求菱形的周长.答案：16.
④分别求
的长.答案：
.
层次2：①求
的值.答案：4.
②求
的值.答案：4.
③求
的值.答案：
.
层次3：①求四边形
的面积.答案：
.
②求
与
的面积和.答案：.
③求四边形的周长的最小值.答案：
.
④求
中点运动的路径长.答案：
.
24.解：(1)第一班上行车到
站用时
小时.
第一班下行车到
站用时小时.
(2)当
时，
.
当
时，
.
(3)由(2)知同时出发的一对上、下行车的位置关于中点对称，设乘客到达站总时间为
分钟，[来源:中国*^&教育@#出版网]
当
时，往站用时30分钟，还需再等下行车5分钟，
，不合题意
当
时，只能往站坐下行车，他离站
千米，则离他右边最近的下行车离站也是千米，这辆下行车离
千米.
如果能乘上右侧第一辆下行车，
，
，∴
，
，
∴符合题意.
如果乘不上右侧第一辆下行车，只能乘右侧第二辆下行车，
，
，
，
∴
，
，
∴符合题意.
如果乘不上右侧第二辆下行车，只能乘右侧第三辆下行车，
，
，
，
∴
，
，不合题意.
∴综上，得
.
当
时，乘客需往站乘坐下行车，
离他左边最近的下行车离站是千米，
离他右边最近的下行车离站也是千米.
如果乘上右侧第一辆下行车，
，
∴
，不合题意.
如果乘不上右侧第一辆下行车，只能乘右侧第二辆下行车，
，
，
，∴
，
，
∴符合题意.
如果乘不上右侧第二辆下行车，只能乘右侧第三辆下行车，
，
，
，
，
∴不合题意.
∴综上，得.
综上所述，，或.
