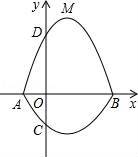
如图，在平面直角坐标系xOy中，A、B为x轴上两点，C、D为y轴上的两点，经过点A、C、B的抛物线的一部分c₁与经过点A、D、B的抛物线的一部分c₂组合成一条封闭曲线，我们把这条封闭曲线成为“蛋线”．已知点C的坐标为（0，），点M是抛物线C₂：y=mx²﹣2mx﹣3m（m＜0）的顶点．

（1）求A、B两点的坐标；

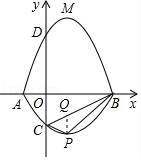
（2）“蛋线”在第四象限上是否存在一点P，使得△PBC的面积最大？若存在，求出△PBC面积的最大值；若不存在，请说明理由；

（3）当△BDM为直角三角形时，求m的值．

答案

解：（1）y=mx²﹣2mx﹣3m，

=m（x﹣3）（x+1），

∵m≠0，

∴当y=0时，x₁=﹣1，x₂=3，

∴A（﹣1，0），B（3，0）；

（2）设C₁：y=ax²+bx+c，将A，B，C三点坐标代入得：

，

解得：，

故C₁：y=x²﹣x﹣；

如图，过点P作PQ∥y轴，交BC于Q，

由B、C的坐标可得直线BC的解析式为y=x﹣，

设p（x， x²﹣x﹣），则Q（x， x﹣），PQ=x﹣﹣（x²﹣x﹣）=﹣x²+x，

S_△PBC=S_△PCQ+S_△PBQ=PQ•OB=×3×（﹣x²+x）=﹣+x=﹣（x﹣）²+，

当x=时，S_max=，

∴P（）

（3）y=mx²﹣2mx﹣3m=m（x﹣1）²﹣4m，

顶点M坐标（1，﹣4m），

当x=0时，y=﹣3m，

∴D（0，﹣3m），B（3，0），

∴DM²=（0﹣1）²+（﹣3m+4m）²=m²+1，

MB²=（3﹣1）²+（0+4m）²=16m²+4，

BD²=（3﹣0）²+（0+3m）²=9m²+9，

当△BDM为直角三角形时，分两种情况：

①当∠BDM=90°时，有DM²+BD²=MB²，

解得m₁=﹣1，m₂=1（∵m＜0，∴m=1舍去）；

②当∠BMD=90°时，有DM²+MB²=BD²，

解得m₁=﹣，m₂=（舍去），

综上，m=﹣1或﹣时，△BDM为直角三角形．