．在平面直角坐标系xOy中，给出如下定义：对于⊙C及⊙C外一点P，M，N是⊙C上两点，当∠MPN最大，称∠MPN为点P关于⊙C的“视角”．直线l与⊙C相离，点Q在直线l上运动，当点Q关于⊙C的“视角”最大时，则称这个最大的“视角”为直线l关于⊙C的“视角”．

（1）如图，⊙O的半径为1，

①已知点A（1，1），直接写出点A关于⊙O的“视角”；已知直线y=2，直接写出直线y=2关于⊙O的“视角”；

②若点B关于⊙O的“视角”为60°，直接写出一个符合条件的B点坐标；

（2）⊙C的半径为1，

①点C的坐标为（1，2），直线l：y=kx+b（k＞0）经过点D（﹣2+1，0），若直线l关于⊙C的“视角”为60°，求k的值；

②圆心C在x轴正半轴上运动，若直线y=x+关于⊙C的“视角”大于120°，直接写出圆心C的横坐标x_C的取值范

围．

答案

【考点】圆的综合题．

【分析】（1）①如图1中，过点A作⊙O的切线，切点分别为E、F．点A关于⊙O的“视角”就是两条切线的夹角．∠MPN就是直接写出直线y=2关于⊙O的“视角”；②由①可知，点P关于⊙O的“视角”为60°，根据对称性即可推出点B坐标．

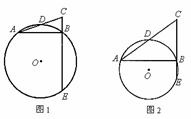
（2）①对于⊙C外的点P，点P关于⊙C的“视角”为60°，则点P在以C为圆心，2为半径的圆上．又直线l关于⊙C的“视角”为60°，此时，点P是直线l上与圆心C的距离最短的点，推出CP⊥直线l，则直线l是以C为圆心，2为半径的圆的一条切线，如图所示．作CH⊥x轴于点H，想办法求出点P坐标即可解决问题．②如图2中，当⊙C与直线y=x+相切时，设切点为P，连接PC则PC⊥AP，想办法求出点C坐标，如图3中，设直线y=x+关于⊙C的“视角”为120°，求出此时的点C坐标，即可解决问题．

【解答】解：（1）①如图1中，过点A作⊙O的切线，切点分别为E、F．

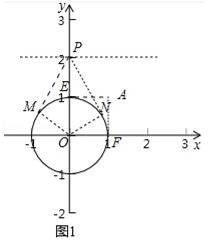
∵A（1，1），⊙O的半径为1，

∴四边形AEOF是正方形，

∴点A关于⊙O的“视角”为∠EAF=90°，

设直线y=2与y轴的交点为P，过点P作⊙O的切线，切点分别为M、N．

在Rt△POM中，∵PO=2OM，

∴∠OPM=30°，同理∠OPA=30°，

∴∠MPN=60°，

∴直线y=2关于⊙O的“视角”为60°，

故答案分别为90°，60°．

②由①可知，点P关于⊙O的“视角”为60°，

∴B（0，2），根据对称性点B得到坐标还可以为（2，0）或（﹣2，0）或（0，﹣2）（本题答案不唯一）

（2）解：①如图1中，

∵直线l：y=kx+b（k＞0）经过点D（﹣2+1，0），

∴（﹣2+1）k+b=0，

∴b=2k﹣k，

∴直线l：y=kx+2k﹣k，

对于⊙C外的点P，点P关于⊙C的“视角”为60°，

则点P在以C为圆心，2为半径的圆上．

又直线l关于⊙C的“视角”为60°，此时，点P是直线l上与圆心C的距离最短的点．

∴CP⊥直线l．

则直线l是以C为圆心，2为半径的圆的一条切线，如图1所示．作CH⊥x轴于点H，

∴点H的坐标为（1，0），

∴DH=．

∴∠CDH=30°，∠PDH=60°，

可求得点P的坐标（﹣+1，3）．

∴3=（﹣+1）k+2k﹣k，

∴k=．

②如图2中，当⊙C与直线y=x+相切时，设切点为P，连接PC则PC⊥AP，

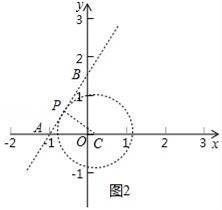
∵直线y=x+与x轴的交点为A（﹣1，0），与y轴的交点为（0，），

∴tan∠BAO==，

∴∠BAO=60°，

∵PC⊥AP，

在Rt△APC中，PC=1，

∴AC=PC÷cos30°=，

∴OC=﹣1，

如图3中，设直线y=x+关于⊙C的“视角”为120°，

作CP⊥AB于P，PE、PF是⊙C的切线，E、F是切点，则∠CPE=60°，PC=CE÷sin60°=，

在Rt△APC中，AC=PC÷sin60°=，

∴OC=﹣1=，

∴直线y=x+关于⊙C的“视角”大于120°时，圆心C的横坐标x_C的取值范围﹣1＜x_C＜．