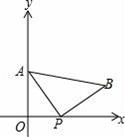
如图，A（0，4）是直角坐标系y轴上一点，动点P从原点O出发，沿x轴正半轴运动，速度为每秒1个单位长度，以P为直角顶点在第一象限内作等腰Rt△APB．设P点的运动时间为t秒．

（1）若AB∥x轴，求t的值；

（2）当t=3时，坐标平面内有一点M，使得以M、P、B为顶点的三角形和△ABP全等，请直接写出点M的坐标；

（3）设点A关于x轴的对称点为,连接，

在点P运动的过程中，∠的度数是否会发生变化，

若不变，请求出∠的度数，若改变，请说明理由。

答案

解：（1）过点B作BC⊥x轴于点C，如图1所示．

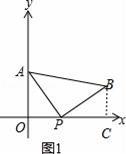
∵AO⊥x轴，BC⊥x轴，且AB∥x轴，

∴四边形ABCO为长方形，

∴AO=BC=4．

∵△APB为等腰直角三角形，

∴AP=BP，∠PAB=∠PBA=45°，

∴∠OAP=90°﹣∠PAB=45°，

∴△AOP为等腰直角三角形，

∴OA=OP=4．

t=4÷1=4（秒），

故t的值为4．                           ------------------------4分

（2）

点M的坐标为（4，7）, （6，-4）, （10，-1）, （0，4）-----------------------8分

（3）答：∠=45°                           ------------------------10分

∵△APB为等腰直角三角形，

∴∠APO+∠BPC=180°﹣90°=90°．

又∵∠PAO+∠APO=90°，

∴∠PAO=∠BPC．

在△PAO和△BPC中，，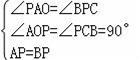

∴△PAO≌△BPC，

∴AO=PC，BC=PO．

∵点A（0，4），点P（t，0）

∴PC=AO=4，BC=PO=t，CO=PC+PO=4+ t

∴点B（4+t，t）                                     ------------------------12分

∴点B在直线y=x﹣4上                            

又∵点A关于x轴的对称点为（0，-4）也在直线y=x﹣4上,

∴∠=45°                                            -