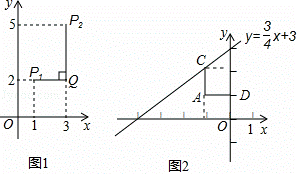
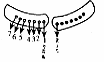
在平面直角坐标系xOy中,对于任意两点P1(x1,y1)与P2(x2,y2)的“非常距离”,给出如下定义:【版权所有:21教育】
若|x1﹣x2|≥|y1﹣y2|,则点P1与点P2的“非常距离”为|x1﹣x2|;
若|x1﹣x2|<|y1﹣y2|,则点P1与点P2的“非常距离”为|y1﹣y2|.
例如:点P1(1,2),点P1(3,5),因为|1﹣3|<|2﹣5|,所以点P1与点P2的“非常距离”为|2﹣5|=3,也就是图1中线段P1Q与线段P2Q长度的较大值(点Q为垂直于y轴的直线P1Q与垂直于x轴的直线P2Q的交点).21教育名师原创作品
(1)已知点A(﹣![]() ),B为y轴上的一个动点,①若点A与点B的“非常距离”为2,写出满足条件的点B的坐标;②直接写出点A与点B的“非常距离”的最小值;
),B为y轴上的一个动点,①若点A与点B的“非常距离”为2,写出满足条件的点B的坐标;②直接写出点A与点B的“非常距离”的最小值;
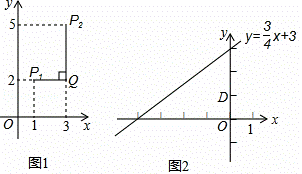
(2)如图2,已知C是直线![]() 上的一个动点,点D的坐标是(0,1),求点C与点D的“非常距离”最小时,相应的点C的坐标.21*cnjy*com
上的一个动点,点D的坐标是(0,1),求点C与点D的“非常距离”最小时,相应的点C的坐标.21*cnjy*com
答案
(1)①∵B为y轴上的一个动点,
∴设点B的坐标为(0,y).
∵|﹣![]() ﹣0|=
﹣0|=![]() ≠2,
≠2,
∴|0﹣y|=2,
解得,y=2或y=﹣2;
∴点B的坐标是(0,2)或(0,﹣2);------------------------4分
②设点B的坐标为(0,y).
∵|﹣![]() ﹣0|≥|0﹣y|,
﹣0|≥|0﹣y|,
∴点A与点B的“非常距离”最小值为|﹣![]() ﹣0|=
﹣0|=![]() ; ------------------------6分
; ------------------------6分
(2)如图2,取点C与点D的“非常距离”的最小值时,需要根据运算定义“若|x1﹣x2|≥|y1﹣y2|,21教育网
则点P1与点P2的“非常距离”为|x1﹣x2|”解答,此时|x1﹣x2|=|y1﹣y2|.
即AC=AD, ------------------------8分
∵C是直线y=![]() x+3上的一个动点,点D的坐标是(0,1),
x+3上的一个动点,点D的坐标是(0,1),
∴设点C的坐标为(x0,![]() x0+3),
x0+3),
∴﹣x0=![]() x0+2, ------------------------10分
x0+2, ------------------------10分
此时,x0=﹣![]() ,
,
∴点C与点D的“非常距离”的最小值为:|x0|=![]() ,
,
此时C(﹣![]() ,
,![]() ). ------------------------12分
). ------------------------12分