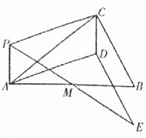
如图1，P为Rt△ABC所在平面内任意一点(不在直线AC上)，∠ACB = 90°，M为AB边中点．

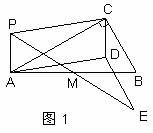
操作：以PA、PC为邻边作平行四边形PADC，连续PM并延长到点E，使ME = PM，连结DE．

探究：⑴请猜想与线段DE有关的三个结论；

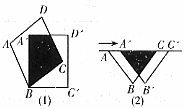
⑵请你利用图2，图3选择不同位置的点P按上述方法操作；

⑶经历⑵之后，如果你认为你写的结论是正确的，请加以证明；

如果你认为你写的结论是错误的，请用图2或图3加以说明；

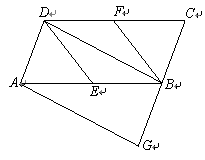
⑷若将“Rt△ABC”改为“任意△ABC”，其他条件不变，利用图4操作，并写出与线

段DE有关的结论(直接写答案)．

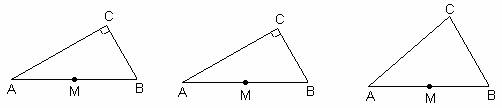
         图2                                                  图3                                   图4

解：（1）DE//BC，DE=BC，DEAC

   （2）如图

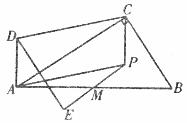
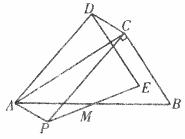
    （3）方法一：

        如图，连结BE，PM=ME，AM=MB，PMA=EMB，

        PMA≌EMB

        PA=BE，MPA=MEB，PA//BE

         四边形DEBC是平行四边形

         DE//BC，DE=BC

          ACB=90，BCAC，DEAC

        方法二：

        如图，连结BE、PB、AE，

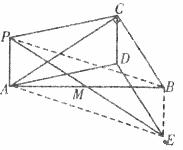
        PA//BE，PA=BE

        余下部分同方法一

        方法三：

        如图，连结PD，交AC于N，连结MN，

        又

        DE//BC，DE=BC

         ACB=90，BCAC，DEAC

     （4）如图，DE//BC，DE=BC