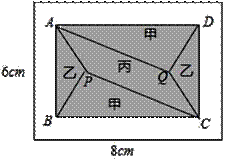
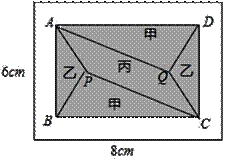
小黄准备给长8m，宽6m的长方形客厅铺设瓷砖，现将其划分成一个长方形ABCD区域Ⅰ（阴影部分）和一个环形区域Ⅱ（空白部分），其中区域Ⅰ用甲、乙、丙三种瓷砖铺设，且满足PQ∥AD，如图所示．

（1）若区域Ⅰ的三种瓷砖均价为300元/m²，面积为S（m²），区域Ⅱ的瓷砖均价为200元/m²，且两区域的瓷砖总价为不超过12000元，求S的最大值；

（2）若区域Ⅰ满足AB：BC=2：3，区域Ⅱ四周宽度相等

①求AB，BC的长；

②若甲、丙两瓷砖单价之和为300元/m²，乙、丙瓷砖单价之比为5：3，且区域Ⅰ的三种瓷砖总价为4800元，求丙瓷砖单价的取值范围．

答案

【考点】C9：一元一次不等式的应用；HE：二次函数的应用；LB：矩形的性质．

【分析】（1）根据题意可得300S+（48﹣S）200≤12000，解不等式即可；

（2）①设区域Ⅱ四周宽度为a，则由题意（6﹣2a）：（8﹣2a）=2：3，解得a=1，由此即可解决问题；

②设乙、丙瓷砖单价分别为5x元/m²和3x元/m²，则甲的单价为（300﹣3x）元/m²，由PQ∥AD，可得甲的面积=矩形ABCD的面积的一半=12，设乙的面积为s，则丙的面积为（12﹣s），由题意12（300﹣3x）+5x•s+3x•（12﹣s）=4800，解得s=，由0＜s＜12，可得0＜＜12，解不等式即可；

【解答】解：（1）由题意300S+（48﹣S）200≤12000，

解得S≤24．

∴S的最大值为24．

（2）①设区域Ⅱ四周宽度为a，则由题意（6﹣2a）：（8﹣2a）=2：3，解得a=1，

∴AB=6﹣2a=4，CB=8﹣2a=6．

②设乙、丙瓷砖单价分别为5x元/m²和3x元/m²，则甲的单价为（300﹣3x）元/m²，

∵PQ∥AD，

∴甲的面积=矩形ABCD的面积的一半=12，设乙的面积为s，则丙的面积为（12﹣s），

由题意12（300﹣3x）+5x•s+3x•（12﹣s）=4800，

解得s=，

∵0＜s＜12，

∴0＜＜12，

∴0＜x＜50，

∴丙瓷砖单价3x的范围为0＜3x＜150元/m²．

【点评】本题考查不等式的应用、矩形的性质等知识，解题的关键是理解题意，学会构建方程或不等式解决实际问题，属于中考常考题型．