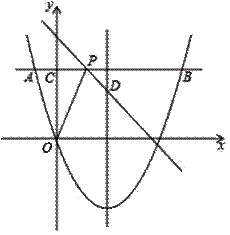
如图，过抛物线y=
x2﹣2x上一点A作x轴的平行线，交抛物线于另一点B，交y轴于点C，已知点A的横坐标为﹣2．
（1）求抛物线的对称轴和点B的坐标；
（2）在AB上任取一点P，连结OP，作点C关于直线OP的对称点D；
①连结BD，求BD的最小值；
②当点D落在抛物线的对称轴上，且在x轴上方时，求直线PD的函数表达式．[中
答案
【考点】HA：抛物线与x轴的交点；H8：待定系数法求二次函数解析式．
【分析】（1）思想确定点A的坐标，利用对称轴公式求出对称轴，再根据对称性可得点B坐标；
（2）①由题意点D在以O为圆心OC为半径的圆上，推出当O、D、B共线时，BD的最小值=OB﹣OD；
②当点D在对称轴上时，在Rt△OD=OC=5，OE=4，可得DE=
=3，求出P、D的坐标即可解决问题；
【解答】解：（1）由题意A（﹣2，5），对称轴x=﹣
=4，
∵A、B关于对称轴对称，
∴B（10，5）．
（2）①如图1中，
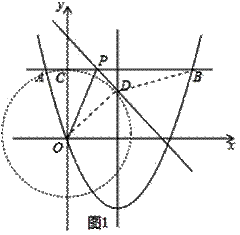
由题意点D在以O为圆心OC为半径的圆上，
∴当O、D、B共线时，BD的最小值=OB﹣OD=
﹣5=5
﹣5．
②如图2中，
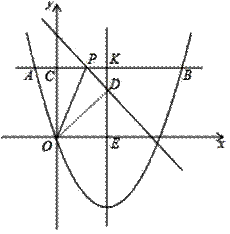
图2
当点D在对称轴上时，在Rt△ODE中，OD=OC=5，OE=4，
∴DE=
=3，
∴点D的坐标为（4，3）．
设PC=PD=x，在Rt△PDK中，x2=（4﹣x）2+22，
∴x=
，
∴P（，5），
∴直线PD的解析式为y=﹣
x+
．
【点评】本题考查抛物线与X轴的交点、待定系数法、最短问题、勾股定理等知识，解题的关键是熟练掌握二次函数的性质，学会利用辅助圆解决最短问题，属于中考常考题型．
