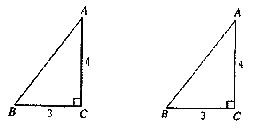
在等腰直角![]() 中,
中,![]() ,
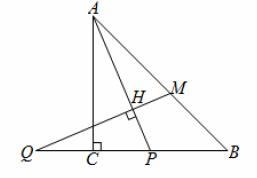
,![]() 是线段
是线段![]() 上一动点(与点
上一动点(与点![]() 不重合),连接
不重合),连接![]() ,延长
,延长![]() 至点
至点![]() ,使得
,使得![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.
(1)若![]() ,求
,求![]() 的大小(用含
的大小(用含![]() 的式子表示).
的式子表示).
(2)用等式表示线段![]() 与
与![]() 之间的数量关系,并证明.
之间的数量关系,并证明.
答案
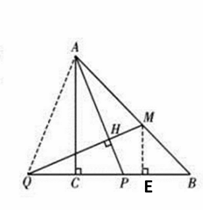

(1) ∠AMQ=45°+![]() .理由如下:
.理由如下:
∵∠PAC=![]() ,△ACB是等腰直角三角形, ∴∠PAB=45°-
,△ACB是等腰直角三角形, ∴∠PAB=45°-![]() ,∠AHM=90°,∴∠AMQ=180°-∠AHM-∠PAM=45°+
,∠AHM=90°,∴∠AMQ=180°-∠AHM-∠PAM=45°+![]() .
.
(2)线段MB与PQ之间的数量关系:PQ=![]() MB.
MB.
理由如下:
连接AQ,过点M做ME⊥QB,
∵AC⊥QP,CQ=CP, ∴∠QAC=∠PAC=![]() ,∴∠QAM=
,∴∠QAM=![]() +45°=∠AMQ, ∴AP=AQ=QM,在RT△APC和RT△QME中,
+45°=∠AMQ, ∴AP=AQ=QM,在RT△APC和RT△QME中,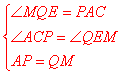 ∴RT△APC≌RT△QME, ∴PC=ME, ∴△MEB是等腰直角三角形,∴
∴RT△APC≌RT△QME, ∴PC=ME, ∴△MEB是等腰直角三角形,∴![]() ,
,
∴PQ=![]() MB.
MB.
考点:全等三角形判定,等腰三角形性质 .