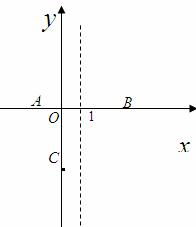
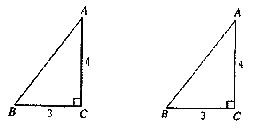
有两个内角分别是它们对角的一半的四边形叫做半对角四边形.
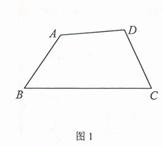
(1)如图1，在半对角四边形
中，
，
，求
与
的度数之和；
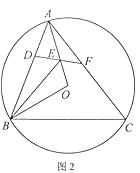
(2)如图2，锐角
内接于
，若边
上存在一点
，使得
，
的平分线交
于点
，连结
并延长交
于点
，
.求证：四边形
是半对角四边形；
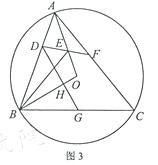
(3)如图3，在(2)的条件下，过点作
于点
，交
于点
，当
时，求
与的面积之比.
答案
（1）120°；（2）证明见解析；（3）
.
【解析】
试题分析：（1）根据四边形内角和等于360°结合已知条件即可求解.
（2）先证明ΔBDE≌ΔBOE,即可证明∠BCE=
∠BDF,连接OC,可证明∠AOC=∠DFC,从而可证四边形DBCF是半对角四边形；
(3)关键是证明ΔDBG∽ΔCBA,得出ΔDBG和ΔABC的面积比，再找出ΔBHG和ΔBDG的面积比，进而求得结论
（2）在ΔBED和ΔBEO中
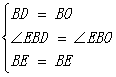[中*@国&%教育出~版网]
∴ΔBED≌ΔBEO
∴∠BDE=∠BOE
又∵∠BCF=∠BOE
∴∠BCF=∠BDE
如图，连接OC
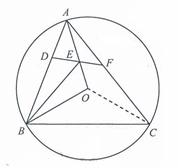
设∠EAF=a，则∠AFE=2∠EAF=2a
∴∠EFC=180°-∠AFE=180°-2a
∵OA=OC
∴∠OAC=∠OCA=a
∴∠AOC=180°-∠OAC-∠OCA=180°-2a
∴∠ABC=∠AOC=∠EFC
∴四边形DBCF是半对角四边形.
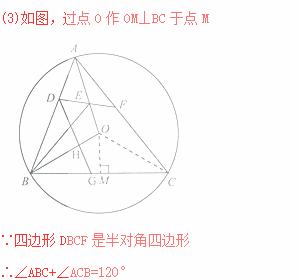
∴∠BAC=60°
∴∠BOC=2∠BAC=120°
∵OB=OC
∴∠OBC=∠OCB=30°
∴BC=2BM=
BO=BD
∵DG⊥OB
∴∠HGB=∠BAC=60°
∵∠DBG=∠CBA
∴ ΔDBG∽ΔCBA
∴
∵DH=BG，BG=2HG
∴DG=3HG
∴
∴
考点：1.四边形内角和；2.圆周角定理；3.相似三角形的判定与性质
