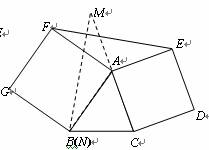
如图，△ABC为锐角三角形，向形外作正方形ACDE和正方形ABGF，连接FE，求证：S_△AFE＝S_△ABC

证明：过点C作CM⊥AB于M，过点E作EN⊥FA交FA的延长线于N，

　　　∴∠AMC＝∠ANE＝90°

　　　∵ACDE是正方形　　∴AE＝AC　∠EAC＝90°　∴∠2＋∠3＝90°

　　又∵ABGF是正方形　　∴∠FAB＝90°　　　∴∠BAN＝90°

　　　∴∠1＋∠2＝90°　　∴∠1＝∠3　　　　　∴Rt△AMC≌Rt△ANE

　　　∴CM＝EN　　　　又∵ABGF是正方形　　∴AF＝AB

　　　S_△AFE＝AF・EN　　S_△ABC＝AB・CM

　　　∴S_△AFE＝S_△ABC

　请你再用另一种方法证明S_△AFE＝S_△ABC.

（过点B作AC的垂线，过F点作AE的垂线与上面证法属同一种方法）

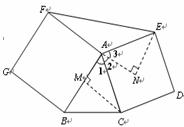
证明：将△AEF绕点A逆时针旋转90°得△AMN，

　∵四边形ACDE和四边形ABGF都是正方形

　∴点M在CA的延长线上，且AM＝AC

　∴点N与点B重合

　∴△AMN与△ABC等底同高

　∴S_△AMN＝S_△ABC

　∴S_△AFE＝S_△ABC