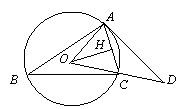
如图,已知⊙O的直径AB垂直弦CD于E,连接AD,BD,OC,OD,且OD=5.
(1)若sin∠BAD=![]() ,求CD的长.
,求CD的长.
(2)若∠ADO:∠EDO=4:1,求扇形OAC(阴影部分)的面积(结果保留![]() ).
).
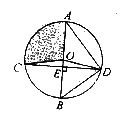
答案
解:(1)![]() .
.
(2) ∵ AB 是⊙O的直径,AB⊥CD,
∴ ![]() =
=![]() ,
, ![]() =
=![]()
∴∠BAD=∠CDB,∠AOC=∠AOD.
由AO=DO,可知∠OAD=∠ADO.
所以∠CDB=∠ADO.
设∠ADO=4x 则∠CDB=4x
由∠ADO:∠EDO=4:1,可知∠EDO=x.
∵∠ADO+∠EDO+∠EDB=90°
∴4x+4x+x=90°解得x=10°.
即∠ADO=40°,∠EDO=10°
∴∠AOC=∠AOD=180°-(∠OAD+∠ADO)=100°.
∴![]()