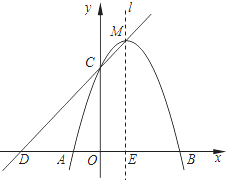
如图,已知在平面直角坐标系xOy中,抛物线![]() 与x轴交于点A(﹣1,0)和点B,与y轴相交于点C(0,3),抛物线的对称轴为直线l.
与x轴交于点A(﹣1,0)和点B,与y轴相交于点C(0,3),抛物线的对称轴为直线l.
(1)求这条抛物线的关系式,并写出其对称轴和顶点M的坐标;
(2)如果直线y=kx+b经过C、M两点,且与x轴交于点D,点C关于直线l的对称点为N,试证明四![]() 边形CDAN是平行四边形;
边形CDAN是平行四边形;
(3)点P在直线l上,且以点P为圆心的圆经过A、B两点,并且与直线CD相切,求点P的坐标.
答案
(1)![]() ,对称轴为直线x=1,顶点M(1,4);(2)证明见解析;(3)P1(1,
,对称轴为直线x=1,顶点M(1,4);(2)证明见解析;(3)P1(1,![]() ),P2(1,
),P2(1,![]() ).
).
 试题解析:(1)∵抛物线
试题解析:(1)∵抛物线![]() 经过点A(﹣1,0)和点C(0,3),∴
经过点A(﹣1,0)和点C(0,3),∴![]() ,∴
,∴![]() ,∴
,∴![]() ,即
,即![]() ,对称轴为直线x=1,顶点M(1,4);
,对称轴为直线x=1,顶点M(1,4);
(2)如图1,∵点C关于直线l的对称点为N,∴N(2,3),∵直线y=kx+b经过C、M两点,∴![]() ,∴
,∴![]() ,∴y=x+3,∵y=x+3与x轴交于点D,∴D(﹣3,0),∴AD=2=CN
,∴y=x+3,∵y=x+3与x轴交于点D,∴D(﹣3,0),∴AD=2=CN
又∵AD∥CN,∴C![]() DAN是平行四边形;
DAN是平行四边形;
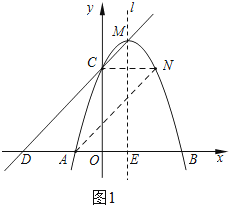
(3)设P(1,a),过点P作PH⊥DM于H,连接PA、PB,如图2,
则MP=4﹣a,又∠HMP=45°,∴HP=AP=![]() ,Rt△APE中,
,Rt△APE中,![]() ,即:
,即:![]() ,解得:
,解得:![]() ,∴P1(1,
,∴P1(1,![]() ),P2(1,
),P2(1,![]() ).
).
考点:二次函数综合题.

 方程有两个不等实数根;
方程有两个不等实数根; 方程有两个相等实数根;
方程有两个相等实数根; 方程没有实数根。
方程没有实数根。 △>0;
△>0; △=0;
△=0; △<0。
△<0。 (△>0)与x轴两交点间的距离的问题。
(△>0)与x轴两交点间的距离的问题。