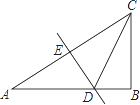
如图，在Rt△ABC中，∠ACB=60°，DE是斜边AC的中垂线，分别交AB、AC于D、E两点．若BD=2，则AC的长是（ ）
A．4 B．
C．8 D．
答案
B．
【解析】
试题分析：如图，∵在Rt△ABC中，∠ACB=60°，∴∠A=30°．
∵DE垂直平分斜边AC，∴AD=CD，∴∠A=∠ACD=30°，∴∠DCB=60°﹣30°=30°，∵BD=2，∴CD=AD=4，∴AB=2+4=6，在△BCD中，由勾股定理得：CB=
，在△ABC中，由勾股定理得：AC=
=，故选B．
考点：线段垂直平分线的性质；含30度角的直角三角形；勾股定理．
