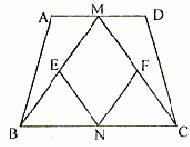
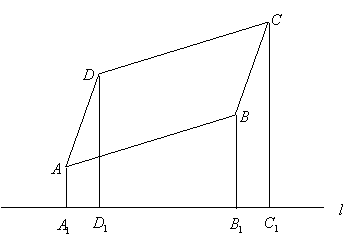
如图l,在等腰梯形ABCD中,AB∥CD,已知AB=12,BC=![]() ,
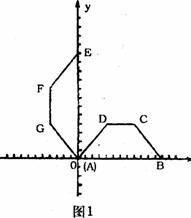
,![]() ,以AB所在的直线为x轴,A为坐标原点建立直角坐标系,将等腰梯形ABCD绕A点按逆时针方向旋转
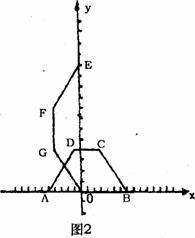
,以AB所在的直线为x轴,A为坐标原点建立直角坐标系,将等腰梯形ABCD绕A点按逆时针方向旋转![]() 得到等腰梯形OEFG(O、E、F、G分别是A、B、C、D旋转后的对应点).
得到等腰梯形OEFG(O、E、F、G分别是A、B、C、D旋转后的对应点).
(1)写出C、F两点的坐标;
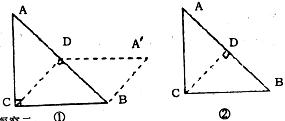
(2)将等腰梯形ABCD沿x轴的负半轴平行移动,设移动后的OA的长度是x,如图2,等腰梯形ABCD与等腰梯形OEFG重合部分的面积为y,当点D移动到与等腰梯形OEFG的内部时.求y与x之间的函数关系式并写出自变量x的取值范围;
(3)当等腰梯形ABCD沿x轴的负半轴平行移动,在直线CD上是否存在点P,使△EFP为等腰三角形?若存在,求出P点的坐标,若不存在,说明理由.
答案
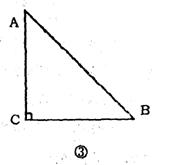
解:(1)过C作CH⊥![]() 于点H
于点H
BC=![]() ,
,![]()
∴CH=BH=4 ∴C点的坐标为(8,4)
同理可得F点坐标为(-4,8).
(2)设AD、DC分别与OG、OE交予点M、N
∠DAB=∠GOA=![]() ,
,
OM=AM=![]() =
=![]() ,ON=4
,ON=4
连结OD,![]() ,
,
即![]()
=![]()
=![]()

(3)设P点坐标为(![]() ,4)
,4)
(Ⅰ)若PE=PF,在Rt△PNE和Rt△PGF中,
由![]()
得![]() 解得
解得![]() =4
=4
(Ⅱ)若PE=EF,![]()
得![]() ,解得
,解得![]() (舍去)
(舍去)
(Ⅲ)若PE=EF,则![]()
得![]() ,化简得
,化简得![]()
方程无解,此时P点不存在.
综合(Ⅰ)、(Ⅱ)、(Ⅲ)知。所求P点坐标为![]() ,
,![]()



 (上底长+下底长)×高。
(上底长+下底长)×高。 
 .
.