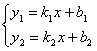某商场经营一批进价为a元/台的小商品,经调查得到下表中的数据:
| 销售价(x元/台) | 35 | 40 | 45 | 50 |
| 日销售量(y台) | 57 | 27 | ||
| 日销售额(t元) | 1680 | |||
| 日销售利润(p元) | 285 | 240 |
(1)请把表中空白处填上适当的数.
(2)在平面直角坐标系中,根据(1)中的数据。描写实数对(x,y)的对应点,并写出y与x的一个函数关系式.
(3)根据(2)中的关系写出p与x的函数关系,并指出当销售价x为多少元时,才能获得最大销售利润.
答案
解:(1)
| 销售价(元/台) | 35 | 40 | 45 | 50 |
| 日销售量(台) | 57 | 42 | 27 | 12 |
| 日销售额(元) | 1995 | 1680 | 1215 | 600 |
| 日销售利润(元) | 285 | 420 | 405 | 240 |
(2)设函数解析式为:![]() ,画出图象如图;
,画出图象如图;
将![]()
![]() 代入
代入![]()
得![]() ,
, ![]()
∴![]()
(3)根据题意,一台小商品的成本为:![]()
![]()
=![]()
当![]() 时,
时,![]()
即当销售价![]() 为42元时.才能获得最大销售利润
为42元时.才能获得最大销售利润