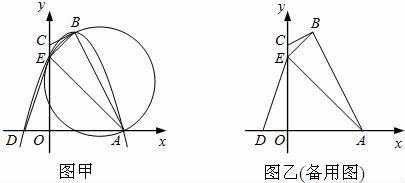
如图甲，四边形OABC的边OA、OC分别在x轴、y轴的正半轴上，顶点在B点的抛物线交x轴于点A、D，交y轴于点E，连接AB、AE、BE．已知tan∠CBE=，A（3，0），D（﹣1，0），E（0，3）．

（1）求抛物线的解析式及顶点B的坐标；

（2）求证：CB是△ABE外接圆的切线；

（3）试探究坐标轴上是否存在一点P，使以D、E、P为顶点的三角形与△ABE相似，若存在，直接写出点P的坐标；若不存在，请说明理由；

（4）设△AOE沿x轴正方向平移t个单位长度（0＜t≤3）时，△AOE与△ABE重叠部分的面积为s，求s与t之间的函数关系式，并指出t的取值范围．

答案

【分析】（1）已知A、D、E三点的坐标，利用待定系数法可确定抛物线的解析式，进而能得到顶点B的坐标．

（2）过B作BM⊥y轴于M，由A、B、E三点坐标，可判断出△BME、△AOE都为等腰直角三角形，易证得∠BEA=90°，即△ABE是直角三角形，而AB是△ABE外接圆的直径，因此只需证明AB与CB垂直即可．BE、AE长易得，能求出tan∠BAE的值，结合tan∠CBE的值，可得到∠CBE=∠BAE，由此证得∠CBA=∠CBE+∠ABE=∠BAE+∠ABE=90°，此题得证．

（3）△ABE中，∠AEB=90°，tan∠BAE=，即AE=3BE，若以D、E、P为顶点的三角形与△ABE相似，那么该三角形必须满足两个条件：①有一个角是直角、②两直角边满足1：3的比例关系；然后分情况进行求解即可．

（4）过E作EF∥x轴交AB于F，当E点运动在EF之间时，△AOE与△ABE重叠部分是个四边形；当E点运动到F点右侧时，△AOE与△ABE重叠部分是个三角形．按上述两种情况按图形之间的和差关系进行求解．

【解答】（1）解：由题意，设抛物线解析式为y=a（x﹣3）（x+1）．

将E（0，3）代入上式，解得：a=﹣1．

∴y=﹣x²+2x+3．

则点B（1，4）．

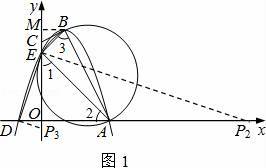
（2）证明：如图1，过点B作BM⊥y于点M，则M（0，4）．

在Rt△AOE中，OA=OE=3，

∴∠1=∠2=45°，AE==3．

在Rt△EMB中，EM=OM﹣OE=1=BM，

∴∠MEB=∠MBE=45°，BE==．

∴∠BEA=180°﹣∠1﹣∠MEB=90°．

∴AB是△ABE外接圆的直径．

在Rt△ABE中，tan∠BAE===tan∠CBE，

∴∠BAE=∠CBE．

在Rt△ABE中，∠BAE+∠3=90°，∴∠CBE+∠3=90°．

∴∠CBA=90°，即CB⊥AB．

∴CB是△ABE外接圆的切线．

（3）解：Rt△ABE中，∠AEB=90°，tan∠BAE=，sin∠BAE=，cos∠BAE=；

若以D、E、P为顶点的三角形与△ABE相似，则△DEP必为直角三角形；

①DE为斜边时，P₁在x轴上，此时P₁与O重合；

由D（﹣1，0）、E（0，3），得OD=1、OE=3，即tan∠DEO==tan∠BAE，即∠DEO=∠BAE

满足△DEO∽△BAE的条件，因此 O点是符合条件的P₁点，坐标为（0，0）．

②DE为短直角边时，P₂在x轴上；

若以D、E、P为顶点的三角形与△ABE相似，则∠DEP₂=∠AEB=90°，sin∠DP₂E=sin∠BAE=；

而DE==，则DP₂=DE÷sin∠DP₂E=÷=10，OP₂=DP₂﹣OD=9

即：P₂（9，0）；

③DE为长直角边时，点P₃在y轴上；

若以D、E、P为顶点的三角形与△ABE相似，则∠EDP₃=∠AEB=90°，cos∠DEP₃=cos∠BAE=；

则EP₃=DE÷cos∠DEP₃=÷=，OP₃=EP₃﹣OE=；

综上，得：P₁（0，0），P₂（9，0），P₃（0，﹣）．

（4）解：设直线AB的解析式为y=kx+b．

将A（3，0），B（1，4）代入，得，解得．

∴y=﹣2x+6．

过点E作射线EF∥x轴交AB于点F，当y=3时，得x=，∴F（，3）．

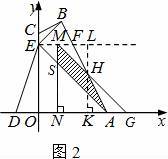
情况一：如图2，当0＜t≤时，设△AOE平移到△GNM的位置，MG交AB于点H，MN交AE于点S．

则ON=AG=t，过点H作LK⊥x轴于点K，交EF于点L．

由△AHG∽△FHM，得，即．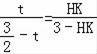

解得HK=2t．

∴S_阴=S_△MNG﹣S_△SNA﹣S_△HAG=×3×3﹣（3﹣t）²﹣t2t=﹣t²+3t．

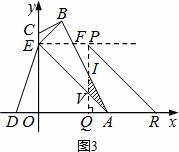
情况二：如图3，当＜t≤3时，设△AOE平移到△PQR的位置，PQ交AB于点I，交AE于点V．

由△IQA∽△IPF，得．即，

解得IQ=2（3﹣t）．

∵AQ=VQ=3﹣t，

∴S_阴=IVAQ=（3﹣t）²=t²﹣3t+．

综上所述：s=．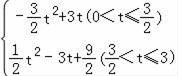

【点评】该题考查了二次函数的综合题，涉及到二次函数解析式的确定、切线的判定、相似三角形的判定、图形面积的解法等重点知识，综合性强，难度系数较大．此题的难点在于后两个小题，它们都需要分情况进行讨论，容易出现漏解的情况．在解答动点类的函数问题时，一定不要遗漏对应的自变量取值范围．