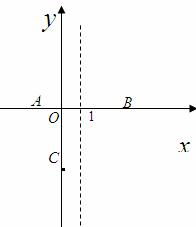
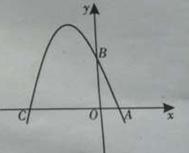
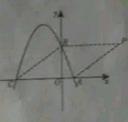
已知如图，在平面直角坐标系xoy中，点A、B、C分别为坐标轴上上的三个点，且OA＝1，OB＝3，OC＝4，
⑴求经过A、B、C三点的抛物线的解析式；
⑵在平面直角坐标系xoy中是否存在一点P，使得以以点A、B、C、P为顶点的四边形为菱形？若存在，请求出点P的坐标；若不存在，请说明理由；
⑶若点M为该抛物线上一动点，在⑵的条件下，请求出当
的最大值时点M的坐标，并直接写出的最大值
答案
⑴解：设抛物线的解析式为
∵A(1，0)、B(0，3)、C(－4，0)∴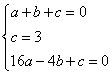
解之
，
，
，∴经过A、B、C三点的抛物线的解析式为
…3分
⑵∵OB＝3，OC＝4，∴BC＝AC＝5，当BP平行且等于AC时，四边形ACBP为菱形∴BP＝AC＝5，且点P到轴的距离等于OB ∴点P的坐标为(5，3) 当点P在第二、三象限时，以点A、B、C、P为顶点的四边形只能是平行四边形，不是菱形，∴当点P的坐标为(5，3)时，以点A、B、C、P为顶点的四边形为菱形…6分
⑶设直线PA的解析式为
∴
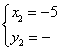解之
，
，∴直线PA的解析式为
……7分，
当点M与点P、A不在同一直线上时，根据三角形的三边关系
，当点M与点P、A在同一直线上时，
，∴当点M与点P、A在同一直线上时，的值最大，即点M为直线PA与抛物线的交点……8分解方程组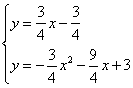
得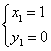
、
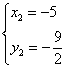∴点M的坐标为(1，0)或(－5，－
)时，的值最大……10分，此时的最大值为5
