如图,AD是△ABC的角平分线, 延长AD交△ABC的外接圆O于点E,过C、D、E三点的圆O1交AC的延长线于点F,连结EF、DF.
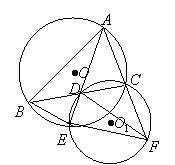
(1)求证:△AEF∽△FED;
(2) 若AD=6,DE=3, 求EF的长;
(3) 若DF∥BE, 试判断△ABE的形状,并说明理由.
答案
解(1)证明:连结两圆的相交弦CE
在圆O1中,∠EFD=∠DCE,
在圆O中,∠BAE=∠DCE,
∴∠EFD=∠BAE,
又因为AE是∠BAC角平分线,得∠BAE=∠CAE,
∴∠CAE=∠EFD,
∵∠AEF=∠FED,
∴△AEF∽△FED.
(2)∵△AEF∽△FED,
∴![]() ,
,
∴EF2=AE・DE=(AD+DE) ・DE=27,
∴![]() .
.
(3)证明:根据同弧上的圆周角相等,
得到:∠ABC=∠AEC,∠CBE=∠CAE,
∴∠ABE=∠AEC+∠CAE,
∵∠AEC+∠CAE+∠ACE=1800=180°,
∴∠ABE+∠ACE=1800,
又∠FCE+∠ACE=1800,∴∠FCE=∠ABE .
∵DF//BE, ∠FDE=∠AEB,,
又∵∠FCE=∠EDF,∴∠AEB =∠ABE ,
∴△ABE为等腰三角形.