如图,已知平行四边形ABCD及四边形外一直线![]() ,四个顶点A、B、C、D到直线
,四个顶点A、B、C、D到直线![]() 的距离分别为a、b、c、d.
的距离分别为a、b、c、d.
(1)观察图形,猜想得出a、b、c、d满足怎样的关系式?证明你的结论.
(2)现将![]() 向上平移,你得到的结论还一定成立吗?请分情况写出你的结论.
向上平移,你得到的结论还一定成立吗?请分情况写出你的结论.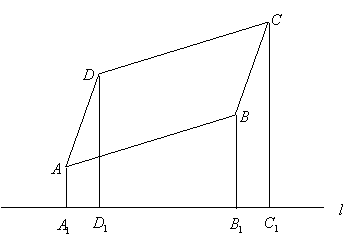
答案
(1)![]() .
.
证明:连结AC、BD,且AC、BD相交于点O,OO0为点O到![]() 的距离,
的距离,
∴OO1为直角梯形BB1D1D的中位线 ,
∴2OO1=DD1+BB1=b+d;
同理:2OO1=AA1+CC1=a+c.
∴![]() .
.
(2)不一定成立.
分别有以下情况:
直线![]() 过A点时,
过A点时,![]() ;
;
直线![]() 过A点与B点之间时,
过A点与B点之间时,![]() ;
;
直线![]() 过B点时,
过B点时,![]() ;
;
直线![]() 过B点与D点之间时,
过B点与D点之间时,![]() ;
;
直线![]() 过D点时,
过D点时,![]() ;
;
直线![]() 过C点与D点之间时,
过C点与D点之间时,![]() ;
;
直线![]() 过C点时,
过C点时,![]() ;
;
直线![]() 过C点上方时,
过C点上方时,![]() .
.


 (上底长+下底长)×高。
(上底长+下底长)×高。 
 .
.