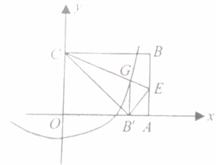
如图(1),已知圆O是等边△ABC的外接圆,过O点作MN//BC分别交AB、AC于M、N,且MN=a。另一个与△ABC全等的等边△DEF的顶点D在MN上移动(不与点M、N重合),并始终保持EF//BC,DF交AB于点P,DE交AC于点Q。
(1)试判断四边形APDQ的形状,并进行证明;
(2)设DM为x,四边形APDQ的面积为y,试探究y与x的函数关系式;四边形APDQ的面积能取到最大值吗?如果能,请求出它的最大值,并确定此时D点的位置。
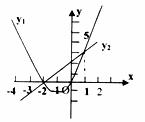
(3)如图(2),当D点和圆心O重合时,请判断四边形APDQ的形状,并说明理由;你能发现四边形APDQ的面积与△ABC的面积有何关系吗?为什么?

答案
(1)可知四边形APDQ为平行四边形
证明:由题知△ABC≌△DEF 且△ABC
△DEF为等边三角形
∴∠BAC=∠EDF=60°
又∵EF//BC,MN//BC
∴EF//BC//MN
∴∠MDF=∠DFE=60°,∠FED=∠EDN=60°
∠MNA=∠BCA=60°,∠QDN=∠QND=60°
∴△DQN为等边三角形
∴∠DQN=∠PDQ=60°,∴PD//AQ
∴∠BAC=∠DQN=60°,∴AP//DQ
∴四边形APDQ为平行四边形
(2)![]()
∴当x取![]() 时,即D点位于MN的中点位置时,四边形APDQ的面积最大,且最大值为
时,即D点位于MN的中点位置时,四边形APDQ的面积最大,且最大值为![]()
(3)当D点和圆心O重合时,四边形APDQ为菱形
理由:由(1)、(2)可知,△MPO,△QON为等边三角形,且MO=ON
所以△MPQ≌△QON
因此OP=OQ,又因为四边形APDQ为平行四边形。
所以可知四边形APDQ为菱形
由题可知,![]() ,而由(2)知
,而由(2)知![]()
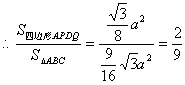
![]()

 (a,b,c是常数,a≠0),那么y叫做x 的二次函数。
(a,b,c是常数,a≠0),那么y叫做x 的二次函数。  (a,b,c是常数,a≠0);
(a,b,c是常数,a≠0);  (a,h,k是常数,a≠0)
(a,h,k是常数,a≠0)  与x轴有交点时,即对应二次好方程
与x轴有交点时,即对应二次好方程 有实根x1和x2存在时,根据二次三项式的分解因式
有实根x1和x2存在时,根据二次三项式的分解因式 ,二次函数
,二次函数 可转化为两根式
可转化为两根式 。如果没有交点,则不能这样表示。
。如果没有交点,则不能这样表示。