我们知道，三角形的三条中线一定会交于一点，这一点就叫做三角形的重心。重心有很多美妙的性质，如有关线段比．面积比就有一些“漂亮”结论，利用这些性质可以解决三角形中的若干问题。

请你利用重心的概念完成如下问题：

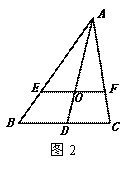
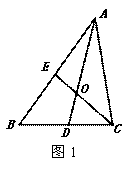
（1）如图1，△ABC的中线AD、CE的交点O为三角形的重心，利用三角形的中位线可以证明：，请你完成该证明；

（2）运用第（1）的结论解决以下问题：

①小丽说：“过三角形的重心任画一条直线都能将三角形的面积平分”。小明想了想说：“这个说法是错误的。”他过点O画出了BC的平行线，交AB、AC于点E、F，如图2，你能求出的值吗？谁的说法正确？

②△ABC中，∠C＝90°，AB=6cm，求△ABC的重心与外心的距离。

答案

解：（1）连DE，                           ………………………………………1分

由题意，D、E为BC、AB中点，

      ∴DE为△ABC的中位线，

      ∴DE∥AC，DE=AC。

      ∴△ODE∽△OAC，且相似比为1:2，     ………………………………………2分

      ∴AO=2OD,∴ ………………………………………………………………3分

（2）①∵EF∥BC，∴△AEO∽△ABD，相似比为。

    ∴…………………………………………………………………………4分

        同理，△AEF∽△ABC，相似比为………………………………………………5分

       ∴，∴……………………………………………………6分

       ∴小明说法正确。…………………………………………………………………7分

②Rt△ABC外心为AB的中点，记为点D，………………………………………8分

     则CD=AB=3，…………………………………………………………………9分

     重心O在中线CD上，由(1)

     ∴OD=3×=1.……………………………………………………………………10分