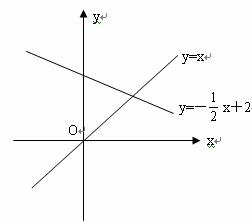
如图,P是y轴上一动点,是否存在平行于y轴的直线x=t,使它与直线y=x和直线![]() 分别交于点D、E(E在D的上方),且△PDE为等腰直角三角形。若存在,求t的值及点P的坐标;若不存在,请说明原因。
分别交于点D、E(E在D的上方),且△PDE为等腰直角三角形。若存在,求t的值及点P的坐标;若不存在,请说明原因。
答案
解:存在。
方法一:当x=t时,y=x=t、当x=t时,![]() 。
。
∴E点的坐标为(t,![]() ),D点坐标为(t,t)。
),D点坐标为(t,t)。
∵E在D的上方,∴![]() ,且t<
,且t<![]() 。
。
∵△PDE为等腰直角三角形,∴PE=DE或PD=DE或PE=PD。
若t>0,PE=DE时,![]() 。
。
∴![]() 。∴P点坐标为(0,
。∴P点坐标为(0,![]() )。
)。
若t>0,PD=DE时,![]() ,
,
∴![]() 。∴P点坐标为(0,
。∴P点坐标为(0,![]() )。
)。
若t>0,PE=PD时,即DE为斜边,∴![]() 。
。
∴![]() ,∴DE的中点的坐标为(t,
,∴DE的中点的坐标为(t,![]() ),
),
∴P点坐标为(0,![]() )。
)。
若t<0,PE=PD时,由已知得DE=-t,![]() ,
,
t=4>0(不符合题意,舍去),此时直线x=t不存在。
若t<0,PE=PD时,即DE为斜边时,由已知得DE=-2t,
![]() ,
,
∴![]() 。∴P点坐标为(0,0)
。∴P点坐标为(0,0)
综上所述:当t=![]() 时,△PDE为等腰直角三角形,此时P点坐标为(0,
时,△PDE为等腰直角三角形,此时P点坐标为(0,![]() )或
)或
(0,![]() );当
);当![]() 时,△PDE为等腰直角三角形,此时P点坐标为(0,
时,△PDE为等腰直角三角形,此时P点坐标为(0,![]() );当t=-4时,△PDE为等腰直角三角形,此时P点坐标为(0,0)。
);当t=-4时,△PDE为等腰直角三角形,此时P点坐标为(0,0)。
方法二:设直线![]() 交y轴于点A,交直线y=x于点B,过B做BM垂直于y轴,垂足为M,交DE于点N。∵x=t平行于y轴,∴MN=
交y轴于点A,交直线y=x于点B,过B做BM垂直于y轴,垂足为M,交DE于点N。∵x=t平行于y轴,∴MN=![]() 。
。
∵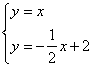 解得
解得![]() ∴B点坐标为(
∴B点坐标为(![]() ,
,![]() ),
),
∴BM=![]()
当x=0时,![]() ,∴A点坐标为(0,2),∴OA=2。
,∴A点坐标为(0,2),∴OA=2。
∵△PDE为等腰直角三角形,∴PE=DE或PD=DE或PE=PD。
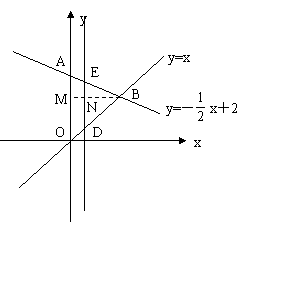 如图,若t>0,PE=DE和PD=DE时,∴PE=t,PD=t,∵DE∥OA,
如图,若t>0,PE=DE和PD=DE时,∴PE=t,PD=t,∵DE∥OA,
∴△BDE∽△BOA,∴![]() ………5分
………5分
∴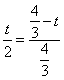 ∴t=
∴t=![]() 。
。
当t=![]() 时,
时,![]() 。
。
∴P点坐标为(0,![]() )或(0,
)或(0,![]() )。…6分
)。…6分
若t>0,PD=PE时,即DE为斜边,∴DE=2MN=2t。
∵DE∥OA,∴△BDE∽△BOA∴![]()
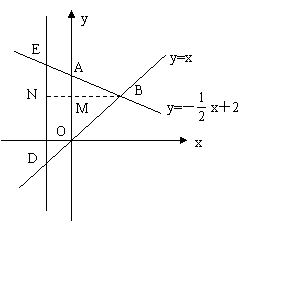 ∴
∴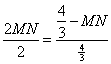 ,∴MN=t=
,∴MN=t=![]() ,
,
DE的中点的纵坐标为![]() 。
。
∴P点的坐标为(0,![]() )
)
如图,若t<0,PE=DE或PD=DE时,
∵DE∥OA,
∴△BDE∽△BOA∴![]() …………9分
…………9分
DE=-4(不符合题意,舍去),此时直线x=t不存在。
若t<0,PE=PD时,即DE为斜边,∴DE=2MN=-2t。
∵DE∥OA,∴△BDE∽△BOA∴![]()
∴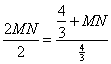 ,∴MN=4,∴t=-4,
,∴MN=4,∴t=-4,![]() 。
。
∴P点坐标为(0,0)
综上所述:当t=![]() 时,△PDE为等腰直角三角形,此时P点坐标为(0,
时,△PDE为等腰直角三角形,此时P点坐标为(0,![]() )或
)或
(0,![]() );当
);当![]() 时,△PDE为等腰直角三角形,此时P点坐标为(0,
时,△PDE为等腰直角三角形,此时P点坐标为(0,![]() );
);
当t=-4时,△PDE为等腰直角三角形,此时P点坐标为(0,0)。