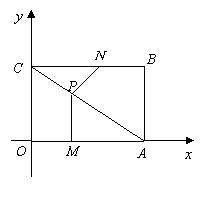
已知A1、A2、A3是抛物线![]() 上的三点,A1B1、A2B2、A3B3分别垂直于x轴,垂足为B1、B2、B3,直线A2B2交线段A1A3于点C。
上的三点,A1B1、A2B2、A3B3分别垂直于x轴,垂足为B1、B2、B3,直线A2B2交线段A1A3于点C。
(1) 如图1,若A1、A2、A3三点的横坐标依次为1、2、3,求线段CA2的长。
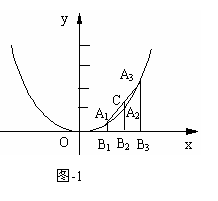
(2)如图2,若将抛物线![]() 改为抛物线
改为抛物线![]() ,A1、A2、A3三点的横坐标为连续整数,其他条件不变,求线段CA2的长。
,A1、A2、A3三点的横坐标为连续整数,其他条件不变,求线段CA2的长。
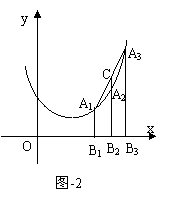
(3)若将抛物线![]() 改为抛物线
改为抛物线![]() ,A1、A2、A3三点的横坐标为连续整数,其他条件不变,请猜想线段CA2的长(用a、b、c表示,并直接写出答案)。
,A1、A2、A3三点的横坐标为连续整数,其他条件不变,请猜想线段CA2的长(用a、b、c表示,并直接写出答案)。
答案
解:(1)∵A1、A2、A3三点的横坐标依次为1、2、3,
∴A1B1= ![]() ,A2B2=
,A2B2=![]() ,A3B3=
,A3B3=![]()
设直线A1A3的解析式为y=kx+b。
∴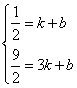 解得
解得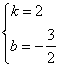
∴直线A1A2的解析式为![]() 。
。
∴CB2=2×2-![]() =
=![]()
∴CA2=CB2-A2B2=![]() -2=
-2=![]() 。
。
(2)设A1、A2、A3三点的横坐标依次n-1、n、n+1。
则A1B1= ![]() ,A2B2=
,A2B2=![]() n2-n+1,
n2-n+1,
A3B3=![]() (n+1)2-(n+1)+1。
(n+1)2-(n+1)+1。
设直线A1A3的解析式为y=kx+b
∴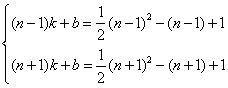
解得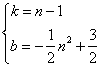
∴直线A1A3的解析式为![]()
∴CB2=n(n-1)-![]() n2+
n2+![]() =
=![]() n2-n+
n2-n+![]()
∴CA2= CB2-A2B2=![]() n2-n+
n2-n+![]() -
-![]() n2+n-1=
n2+n-1=![]() 。
。
(3)当a>0时,CA2=a;当a<0时,CA2=-a