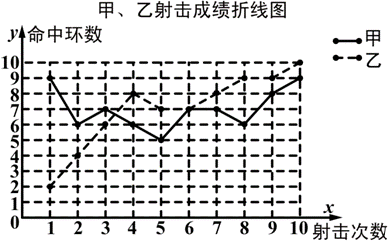
为了从甲、乙两名选手中选拔一个参加射击比赛，现对他们进行一次测验，两个人在相同条件下各射靶10次，为了比较两人的成绩，制作了统计表和统计图：
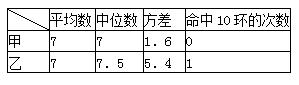
甲、乙射击成绩统计表
| 平均数 | 中位数 | 方差 | 命中10环的次数 | |
| 甲 | 7 | 0 | ||
| 乙 | 1 |
（1）请补全上述图表（直接在表中填空和补全折线图）；
（2）如果规定成绩较稳定者胜出，你认为谁应胜出？说明你的理由；
（3）如果希望（2）中的另一名选手胜出，根据图表中的信息，应该制定怎样的评判规则？为什么？
答案
（1）甲、乙射击成绩统计表
（2）甲
（3）希望乙胜出，规则为命中9环与10环的总数大的胜出．因为乙命中9环与10环的总数为3次，而甲只命中2次．
【解析】
（1）根据折线统计图得乙的射击成绩为2，4，6，7，7，8，8，9，9，10，则平均数为
，中位数为7．5，方差为
×[（2－7）2＋（4－7）2＋（6－7）2＋（8－7）2＋（7－7）2＋（7－7）2＋（8－7）2＋（9－7）2＋（9－7）2＋（10－7）2]＝5．4；
由表知甲的射击成绩的平均数为7，则甲第8次射击成绩为70－（9＋6＋7＋6＋5＋7＋7＋8＋9）＝6（环），故10次射击成绩为5，6，6，6，7，7，7，8，9，9，中位数为7，方差为×[（5－7）2＋（6－7）2＋（6－7）2＋（6－7）2＋（7－7）2＋（7－7）2＋（7－7）2＋（8－7）2＋（9－7）2＋（9－7）2]＝1．6，补全图表如下：
甲、乙射击成绩统计表
（2）因为两人射击成绩的平均数相同，但甲的方差小于乙的方差，故甲胜出．
（3）希望乙胜出，规则为命中9环与10环的总数大的胜出．因为乙命中9环与10环的总数为3次，而甲只命中2次．
【难度】困难
