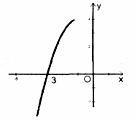
已知:关于x的方程![]() 有两个不相等的实数根
有两个不相等的实数根![]() 和
和![]() ,并且抛物线
,并且抛物线![]() 与x轴的两个交点分别位于点(2,0)的两旁。
与x轴的两个交点分别位于点(2,0)的两旁。
(1)求实数a的取值范围;
(2)当![]() 时,求a的值。
时,求a的值。
答案
(1)解法一:∵关于x的方程![]() 有两个不相等的实数根
有两个不相等的实数根
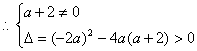
解得:![]() ,且
,且![]()
设抛物线![]() 与x轴的两个交点的坐标分别为
与x轴的两个交点的坐标分别为
![]() 、
、![]() ,且
,且![]()
∴α、β是关于x的方程![]() 的两个不相等的实数根
的两个不相等的实数根
![]()
∴a为任意实数
由根与系数关系得:![]()
∵抛物线![]() 与x轴的两个交点分别位于点(2,0)的两旁
与x轴的两个交点分别位于点(2,0)的两旁
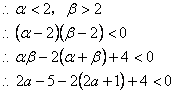
解得:![]()
由<1>、<2>、<3>得 a的取值范围是![]()
解法二:同解法一,得:![]() ,且
,且![]()
∵抛物线![]() 与x轴的两个交点分别位于点(2,0)两旁,
与x轴的两个交点分别位于点(2,0)两旁,
且抛物线的开口向上
∴当![]() 时,
时,![]()
![]()
解得:![]()
由<1>、<2>得 a的取值范围是![]()
(2)解:∵![]() 和
和![]() 是关于x的方程
是关于x的方程![]() 的两个不相等的实数根
的两个不相等的实数根
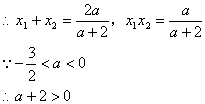
![]()
不妨设![]()
![]()
![]() ,即
,即![]()
![]()
解这个方程,得:![]()
经检验,![]() 都是方程
都是方程![]() 的根
的根
![]() ,舍去
,舍去 ![]() 为所求
为所求

 方程有两个不等实数根;
方程有两个不等实数根; 方程有两个相等实数根;
方程有两个相等实数根; 方程没有实数根。
方程没有实数根。 △>0;
△>0; △=0;
△=0; △<0。
△<0。 (△>0)与x轴两交点间的距离的问题。
(△>0)与x轴两交点间的距离的问题。